Day 11
Math 216: Statistical Thinking
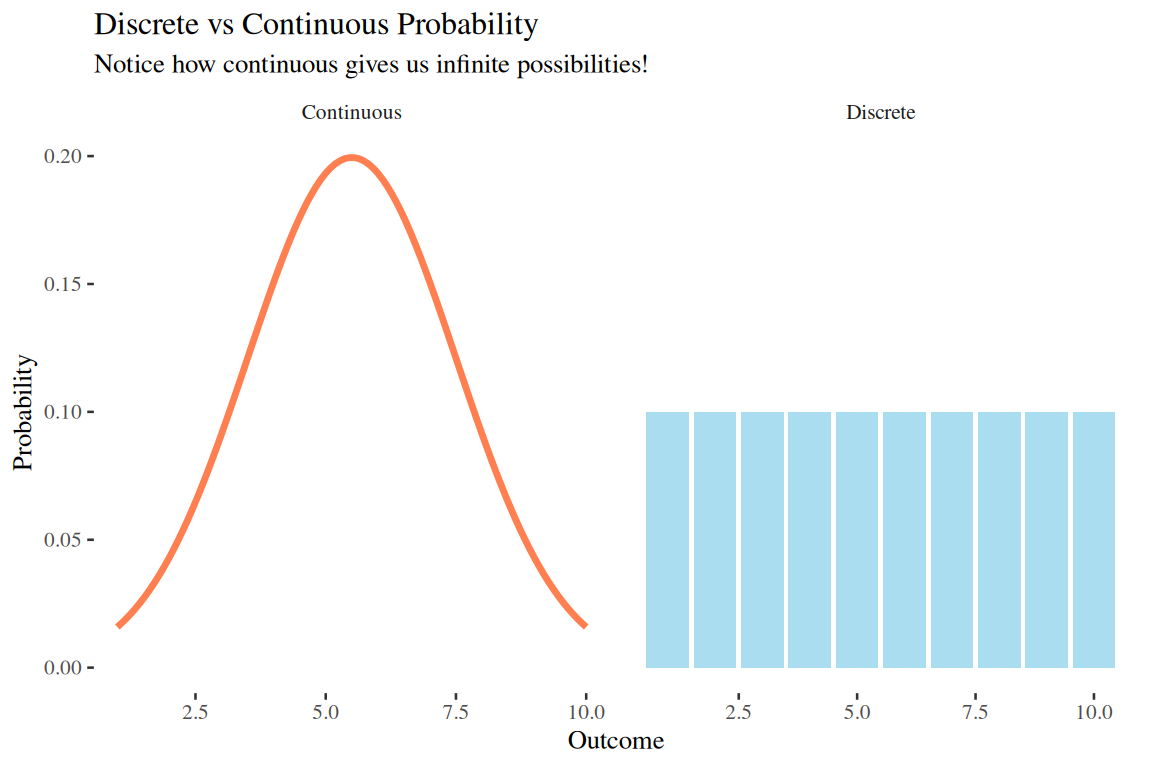
Why Continuous Variables Matter: The Real World is Continuous!
Think about it: Your height isn’t exactly 68 inches, it’s 68.2, 67.8, or 68.0000001 inches! The world around us is beautifully continuous, and we need powerful tools to understand it.
From Discrete to Continuous: A Journey of Understanding
The Magic of Continuity:
- Discrete: Countable outcomes (like dice rolls)
- Continuous: Infinite possibilities (like your exact height)
- The Bridge: As we get more data points, histograms become smooth curves!
Introduction to Continuous Probability Distributions
Continuous random variables are the backbone of modeling real-world phenomena where outcomes can take any value within a range. Unlike discrete variables, which deal with countable outcomes, continuous variables are described by smooth curves called Probability Density Functions (PDFs).
Key Features of PDFs
- Area as Probability: The probability that \(X\) falls between \(a\) and \(b\) is the area under the PDF curve between these points.
- Non-negativity: \(f(x) \geq 0\) for all \(x\).
- Total Probability: The integral of \(f(x)\) over its entire range equals 1, representing certainty.
- Zero Probability at a Point: For continuous variables, \(P(X = a) = 0\) for any specific value \(a\). Probabilities are only meaningful over intervals.
Visualizing Continuous Distributions
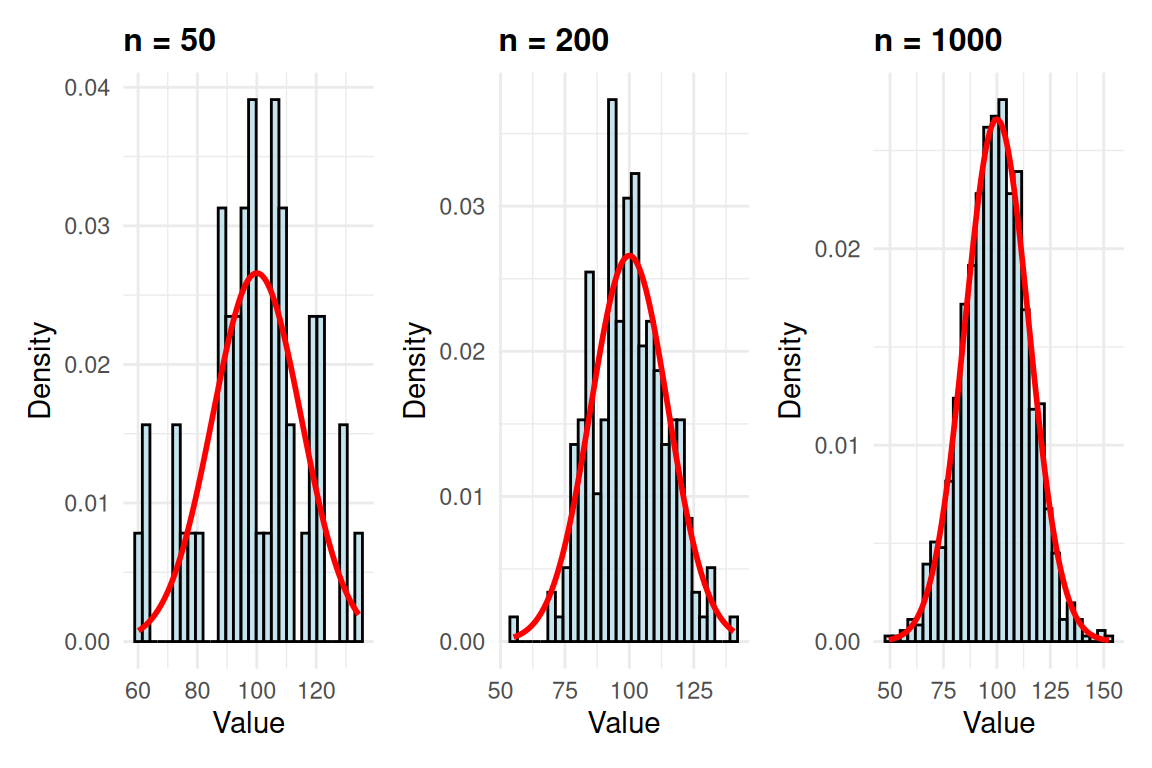
Empirical Probability: As we collect more data, our histogram approaches the true probability density function!
The Magic of Large Samples: Notice how n=1000 gives us a nearly perfect match to our theoretical curve.
Your Observation: What do you notice about the relationship between sample size and curve smoothness?
Calculus Meets Probability
The Beautiful Connection: In continuous probability, we use calculus to find probabilities!
\[P(a \leq X \leq b) = \int_a^b f(x)\,dx\]
What this means: The probability equals the area under the curve between points a and b!
The Uniform Distribution
Definition
The uniform distribution models scenarios where every outcome in a range is equally likely. It’s the simplest continuous distribution, yet it’s incredibly useful in practice.
- PDF: \(f(x) = \frac{1}{b-a}\) for \(x \in [a, b]\).
- Graphical Representation: A flat rectangle, reflecting equal probability density across the range.
Visualizing and Calculating Probabilities
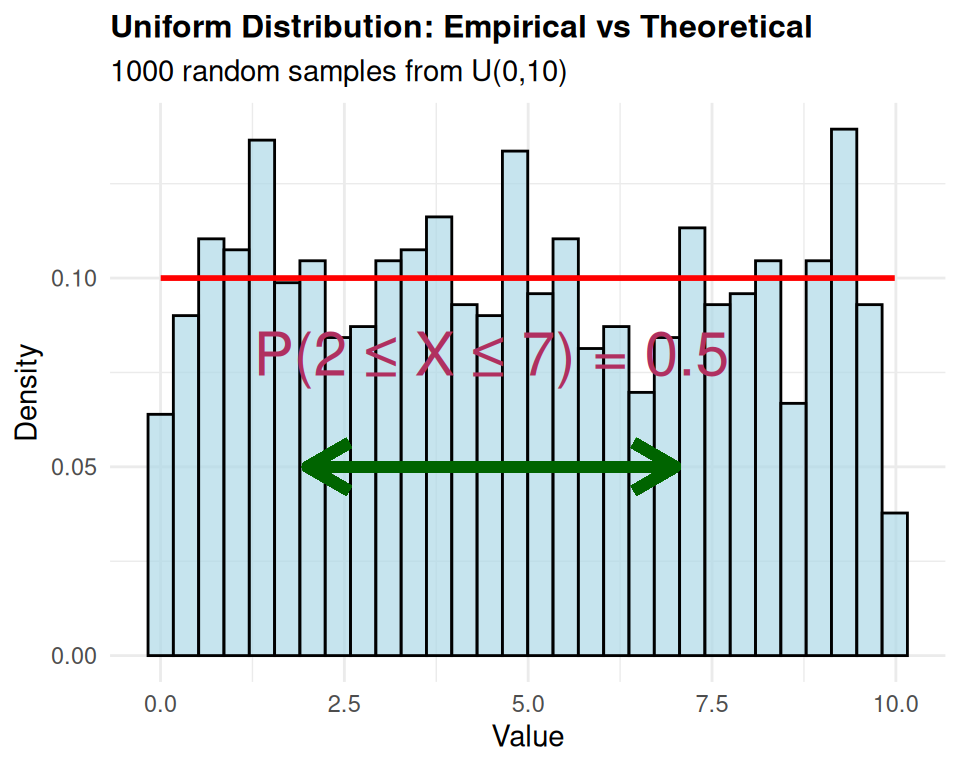
Why Use the Uniform Distribution?
Equal Likelihood:
It’s ideal for modeling fair processes.
Easy Calculations:
Probabilities are straightforward to compute. For example, \(P(a \leq X \leq b) = (b-a) \times \frac{1}{d-c}\).
Empirical Evidence:
Notice how our histogram matches the theoretical flat line
Statistical Measures of \(Unif(a,b)\)
Mean and Median: Both are located at the center of the interval: \(\mu = \frac{a+b}{2}\).
Variance: The spread of the distribution is \(\sigma^2 = \frac{(b-a)^2}{12}\). A wider range leads to greater variability.
Empirical Verification: Try calculating these from our sample data above - do they match the theoretical values?