Day 13

Math 216: Statistical Thinking

Bastola

Why Normality Assessment Matters

Think about it: You assume your data is normal when using statistical tests, but what if it’s not? Your conclusions could be completely wrong! It’s like using a ruler to measure temperature - wrong tool, wrong results.

Theory Vs. Reality: When Normal Goes Wrong

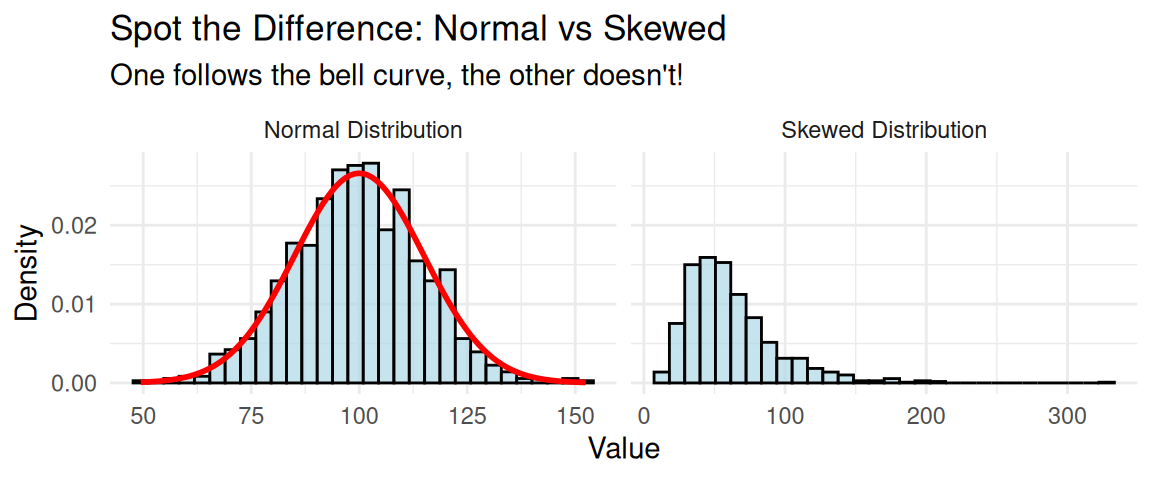
Normal: Symmetric bell shape, balanced tails
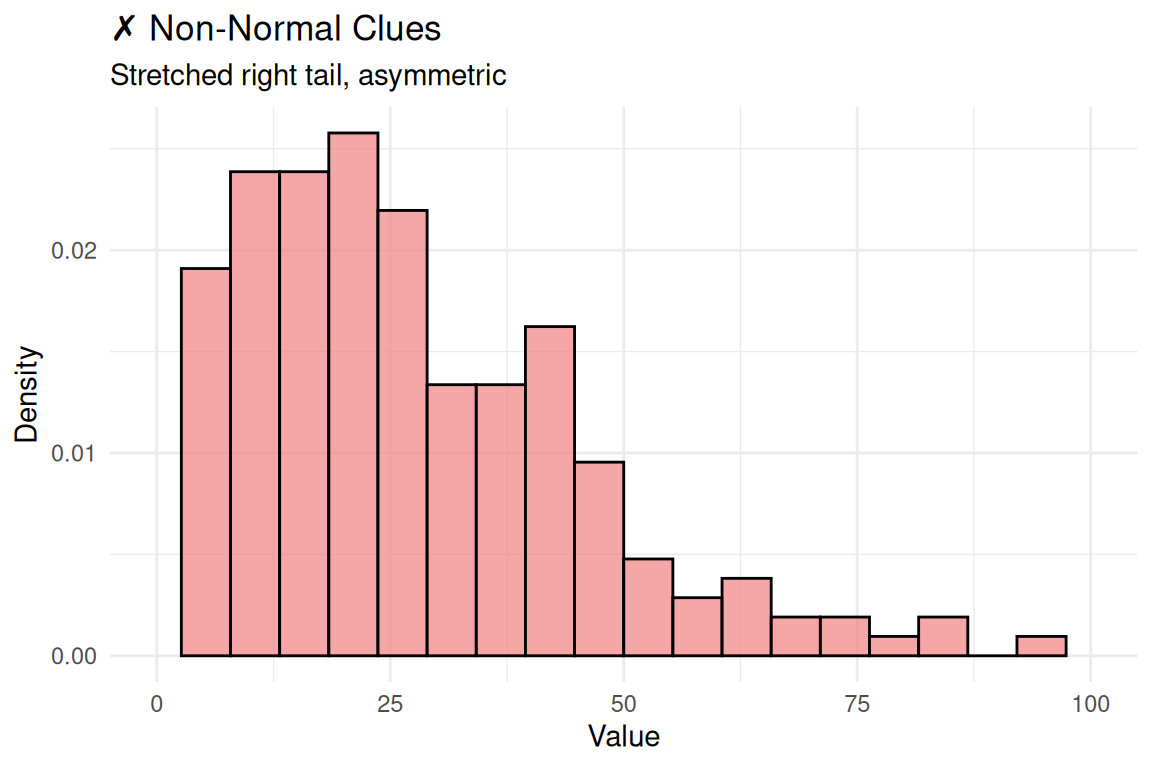
Skewed: Stretched tail on one side - clues to non-normality!

The Danger: Using normal-based tests on skewed data = unreliable results

Three Powerful Methods to Catch Non-Normality:

Visual Detective Work: Plots reveal hidden patterns
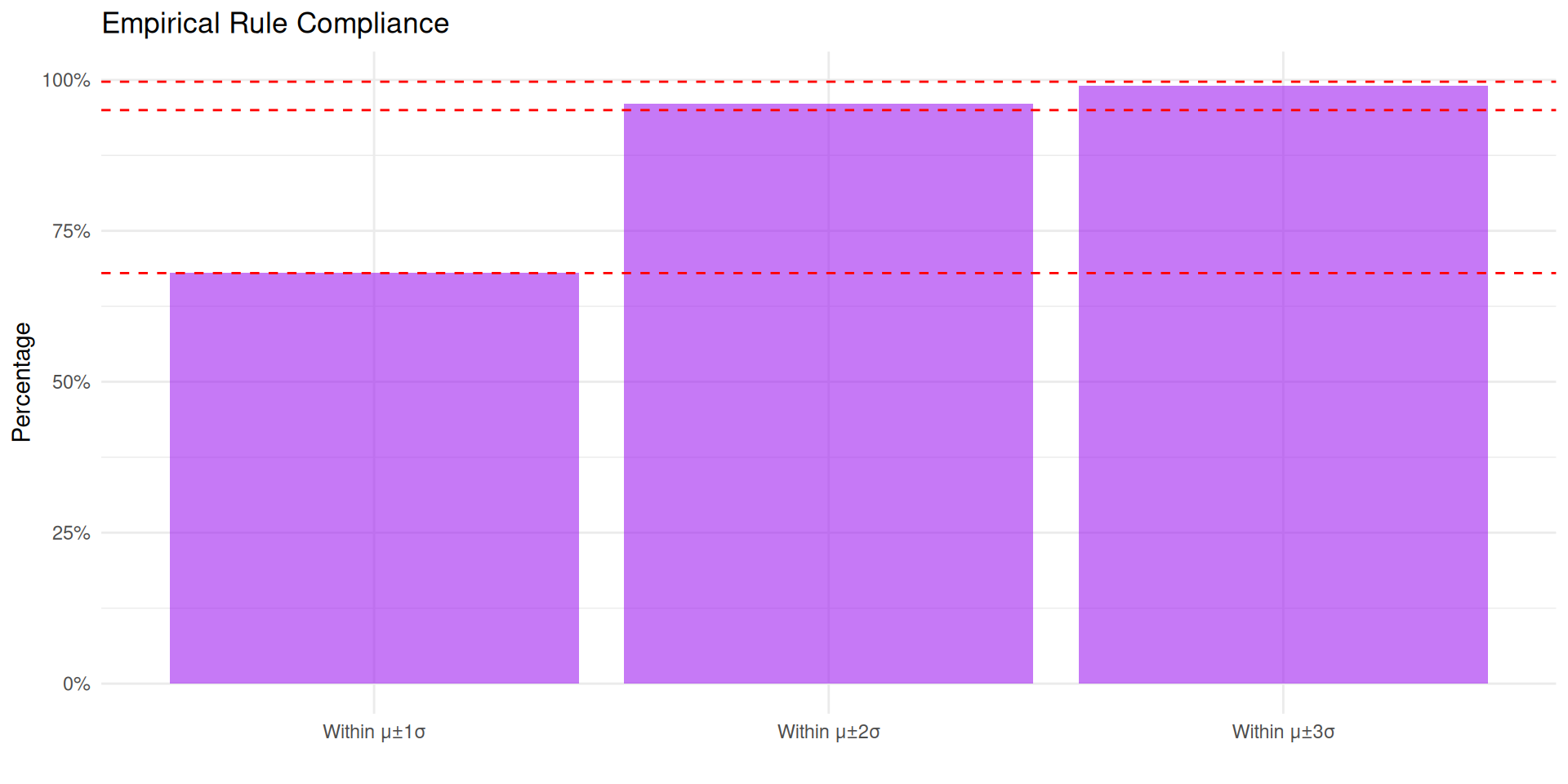
Empirical Rule Check: Does 68-95-99.7% rule hold?
IQR/SD Ratio Test: Quick numerical check (should ≈ 1.3)

Remember: One method isn’t enough - use them together like detective tools!

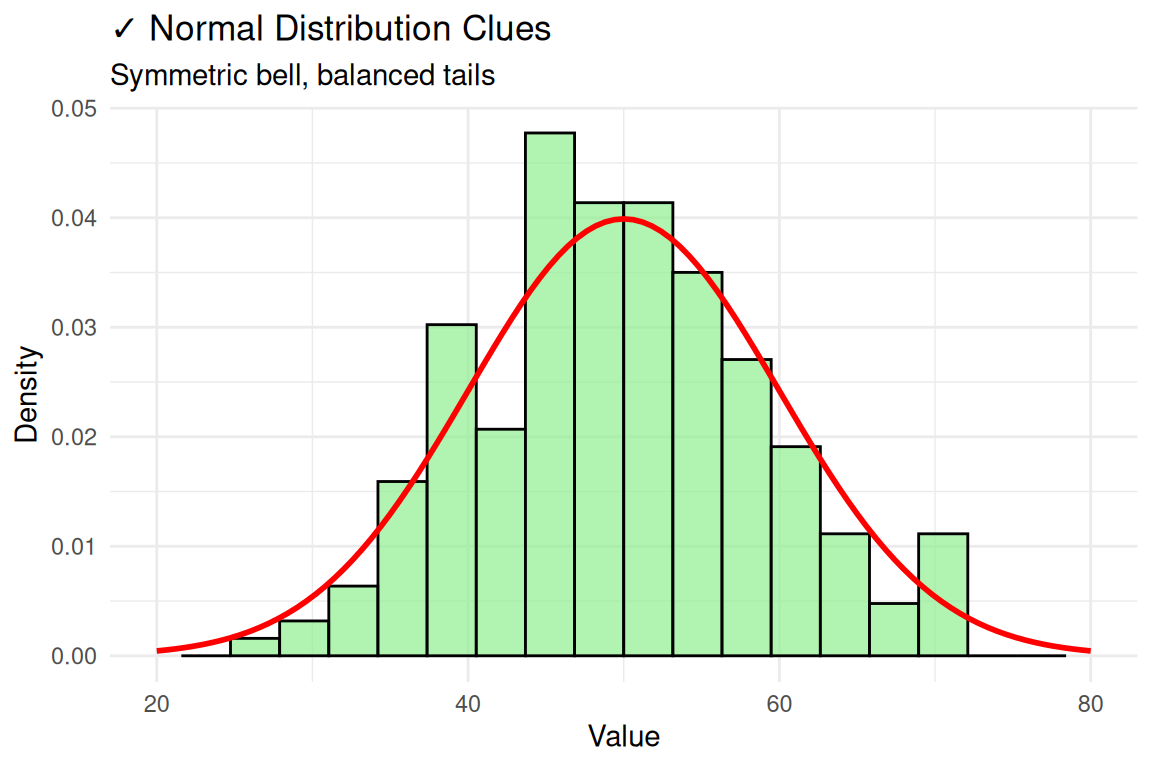
Visual Detective Work: Spot the Clues!

The 3-Step Normality Test

Step 1: Visual Inspection (30 seconds)

Histogram: Bell-shaped? Symmetric?
Q-Q Plot: Points on diagonal?

Step 2: Empirical Rule Check (1 minute)

68% within μ ± 1σ?
95% within μ ± 2σ?
99.7% within μ ± 3σ?

Step 3: IQR/SD Ratio (30 seconds)

Calculate: IQR ÷ SD
Normal data: Ratio ≈ 1.3
Far from 1.3? Red flag!

Quick Rule: If any step fails → investigate further!

Case Study: EPA ratings

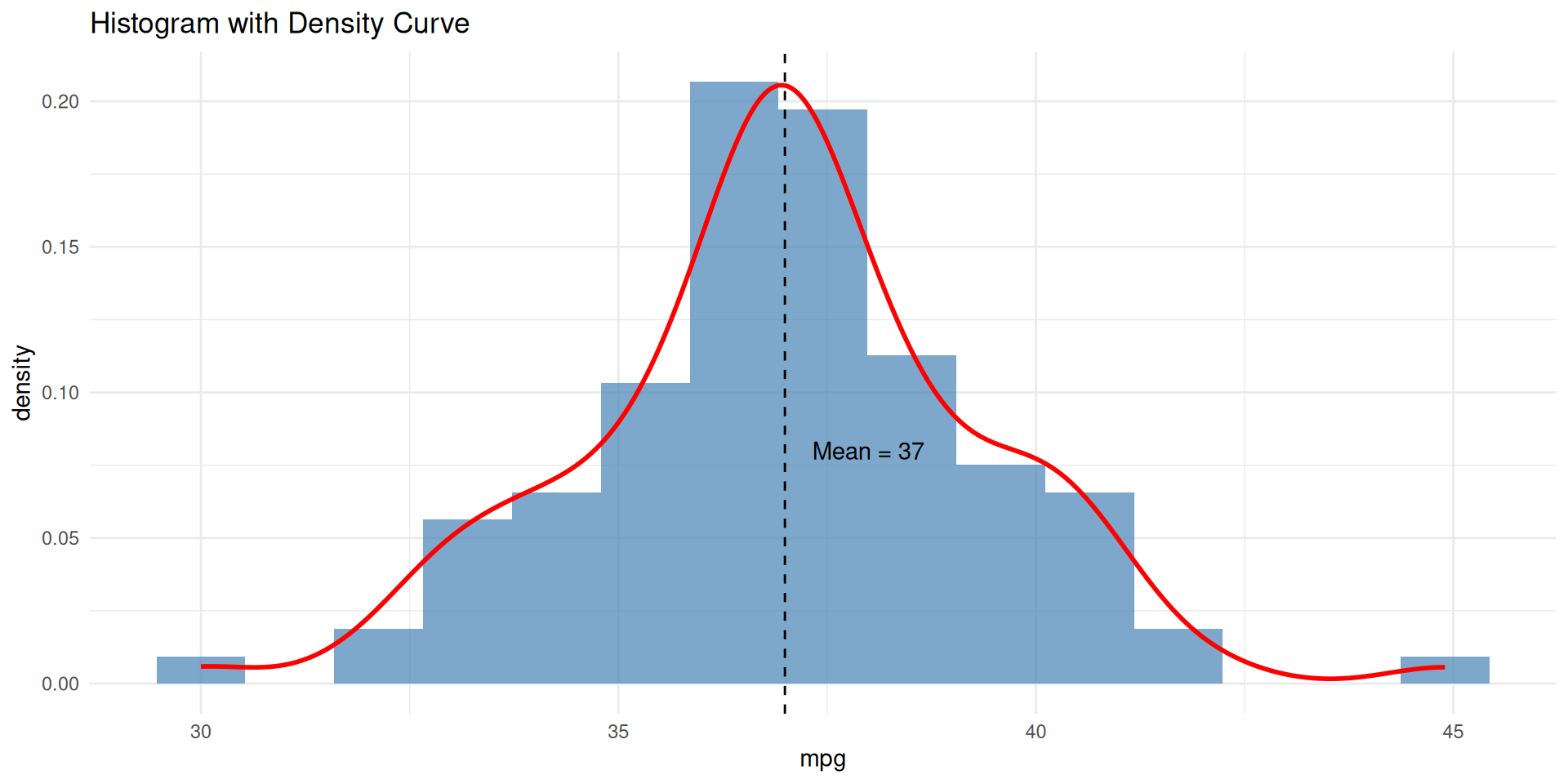
The dataset consists of EPA gas mileage ratings for 100 cars. Each value represents the miles per gallon (MPG) that a particular car achieves under standardized testing conditions. This dataset can help understand how statistical methods are applied in real-world scenarios like assessing the fuel efficiency of vehicles.

Data
R code

EPA Gas Mileage Ratings for 100 Cars (miles per gallon)

col1	col2	col3	col4	col5	col6	col7	col8	col9	col10
36.3	41.0	36.9	37.1	44.9	36.8	30.0	37.2	42.1	36.7
32.7	37.3	41.2	36.6	32.9	36.5	33.2	37.4	37.5	33.6
40.5	36.5	37.6	33.9	40.2	36.4	37.7	37.7	40.0	34.2
36.2	37.9	36.0	37.9	35.9	38.2	38.3	35.7	35.6	35.1
38.5	39.0	35.5	34.8	38.6	39.4	35.3	34.4	38.8	39.7
36.3	36.8	32.5	36.4	40.5	36.6	36.1	38.2	38.4	39.3
41.0	31.8	37.3	33.1	37.0	37.6	37.0	38.7	39.0	35.8
37.0	37.2	40.7	37.4	37.1	37.8	35.9	35.6	36.7	34.5
37.1	40.3	36.7	37.0	33.9	40.1	38.0	35.2	34.8	39.5
39.9	36.9	32.9	33.8	39.8	34.0	36.8	35.0	38.1	36.9

# store 100 mpgs in an object called 'mpg'
mpg <- c(
  36.3, 41.0, 36.9, 37.1, 44.9, 36.8, 30.0, 37.2, 42.1, 36.7,
  32.7, 37.3, 41.2, 36.6, 32.9, 36.5, 33.2, 37.4, 37.5, 33.6,
  40.5, 36.5, 37.6, 33.9, 40.2, 36.4, 37.7, 37.7, 40.0, 34.2,
  36.2, 37.9, 36.0, 37.9, 35.9, 38.2, 38.3, 35.7, 35.6, 35.1,
  38.5, 39.0, 35.5, 34.8, 38.6, 39.4, 35.3, 34.4, 38.8, 39.7,
  36.3, 36.8, 32.5, 36.4, 40.5, 36.6, 36.1, 38.2, 38.4, 39.3,
  41.0, 31.8, 37.3, 33.1, 37.0, 37.6, 37.0, 38.7, 39.0, 35.8,
  37.0, 37.2, 40.7, 37.4, 37.1, 37.8, 35.9, 35.6, 36.7, 34.5,
  37.1, 40.3, 36.7, 37.0, 33.9, 40.1, 38.0, 35.2, 34.8, 39.5,
  39.9, 36.9, 32.9, 33.8, 39.8, 34.0, 36.8, 35.0, 38.1, 36.9
)

mpg_data <- data.frame(mpg = mpg)

Normality Assessment

Q-Q Plot Diagnostics
Empirical Rule Check
IQR/SD Ratio Test

IQR	SD	Ratio	Expected	Difference
2.65	2.42	1.1	1.3	-0.2

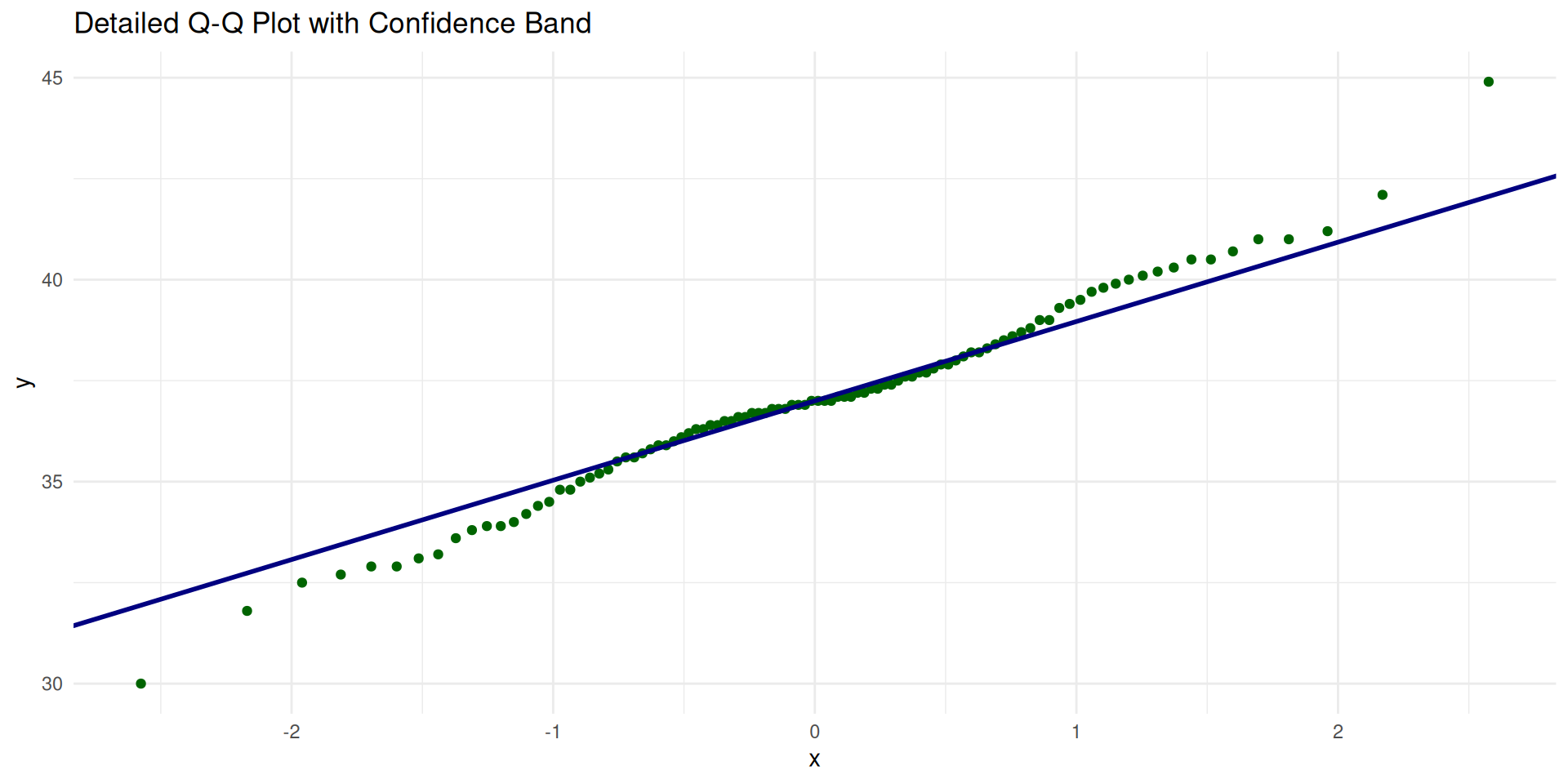
Reading Q-Q Plots: A Detailed Example

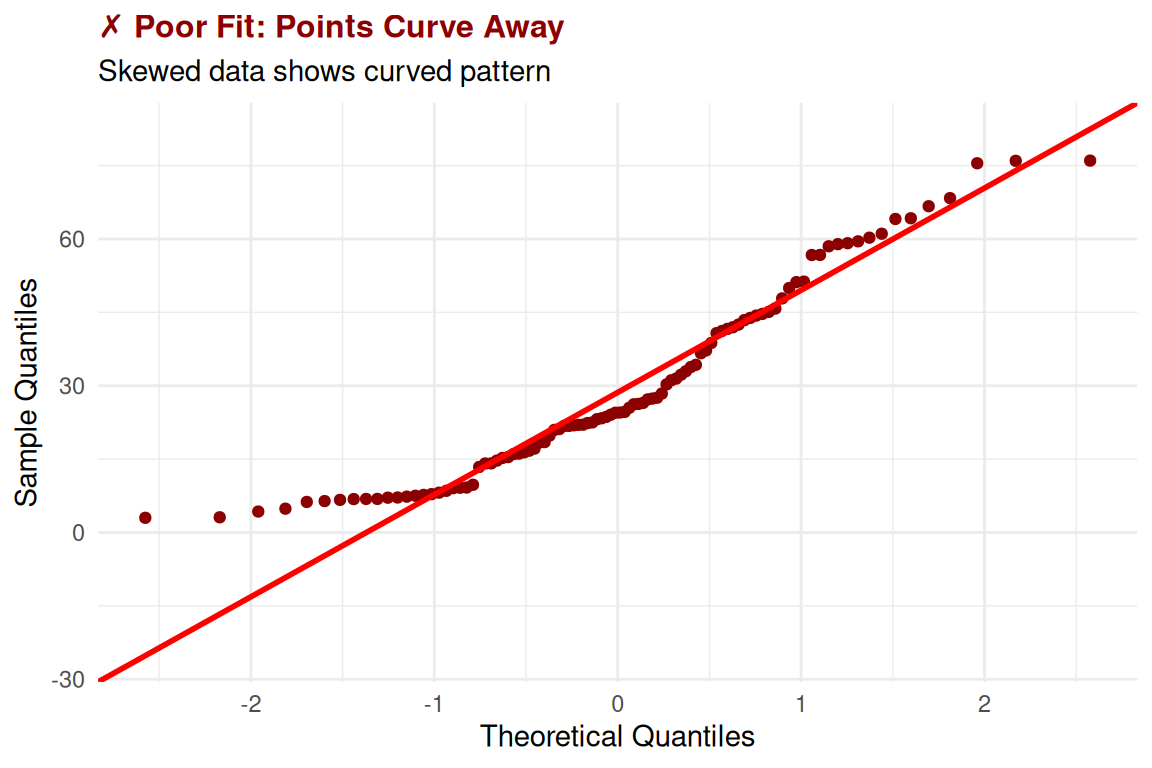
Q-Q Plot Detective Guide

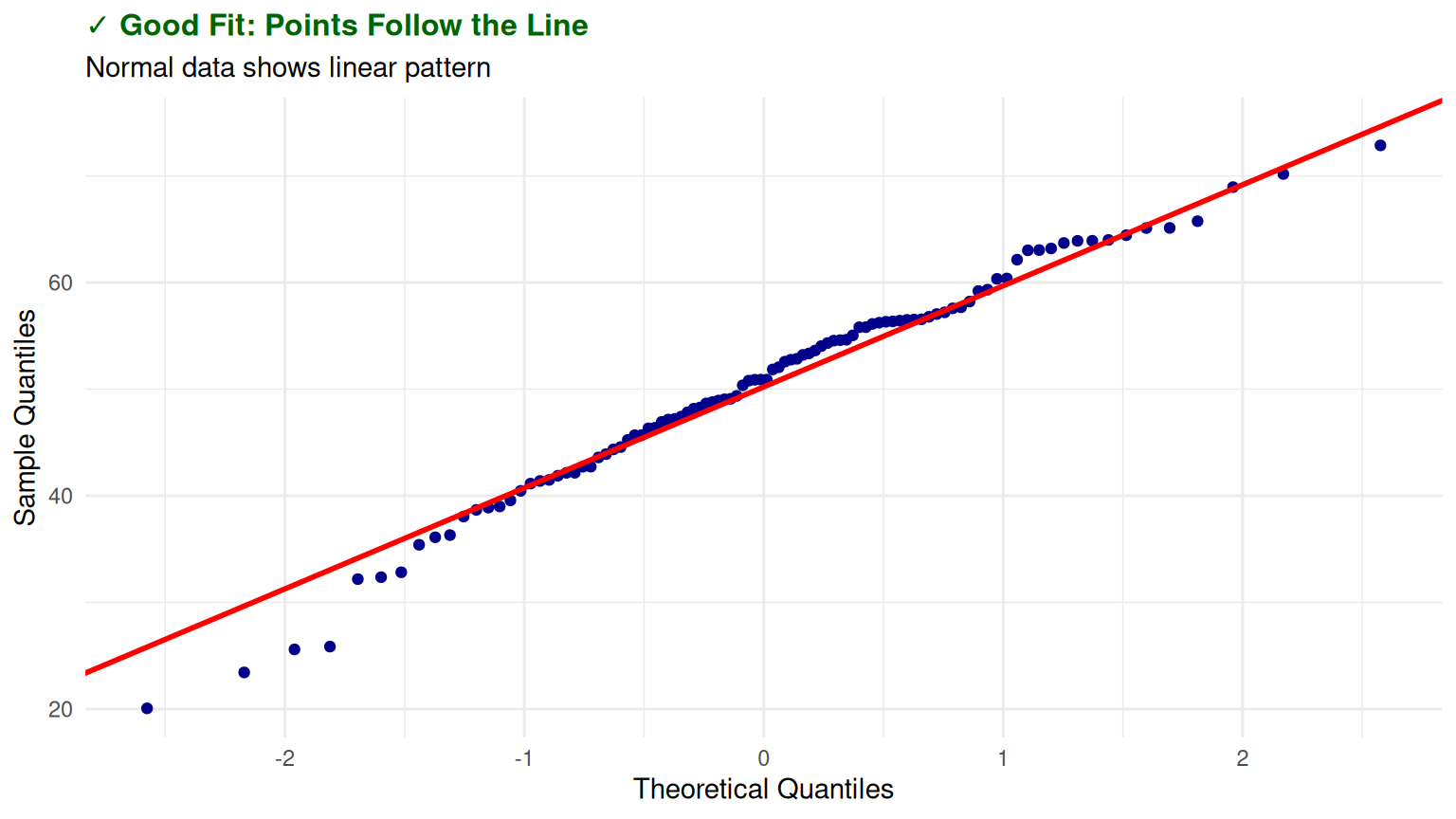
Perfect Alignment (Points hug the red line)

What it means: Your data follows a normal distribution
Action: Safe to use normal-based statistical tests

Curved Patterns (Points form a smile or frown)

What it means: Skewed data (right or left)
Action: Consider log or square root transformation

S-Shaped Curves (Points make an S-curve)

What it means: Heavy or light tails
Action: Check for outliers or consider robust methods

Remember: The Q-Q plot is your normality lie detector test!

EPA Case Study: Detective Work in Action

Our Investigation Results:

Visual Evidence (The Smoking Gun)

Histogram: Right skew detected!
Q-Q plot: Points drift off diagonal in upper tail
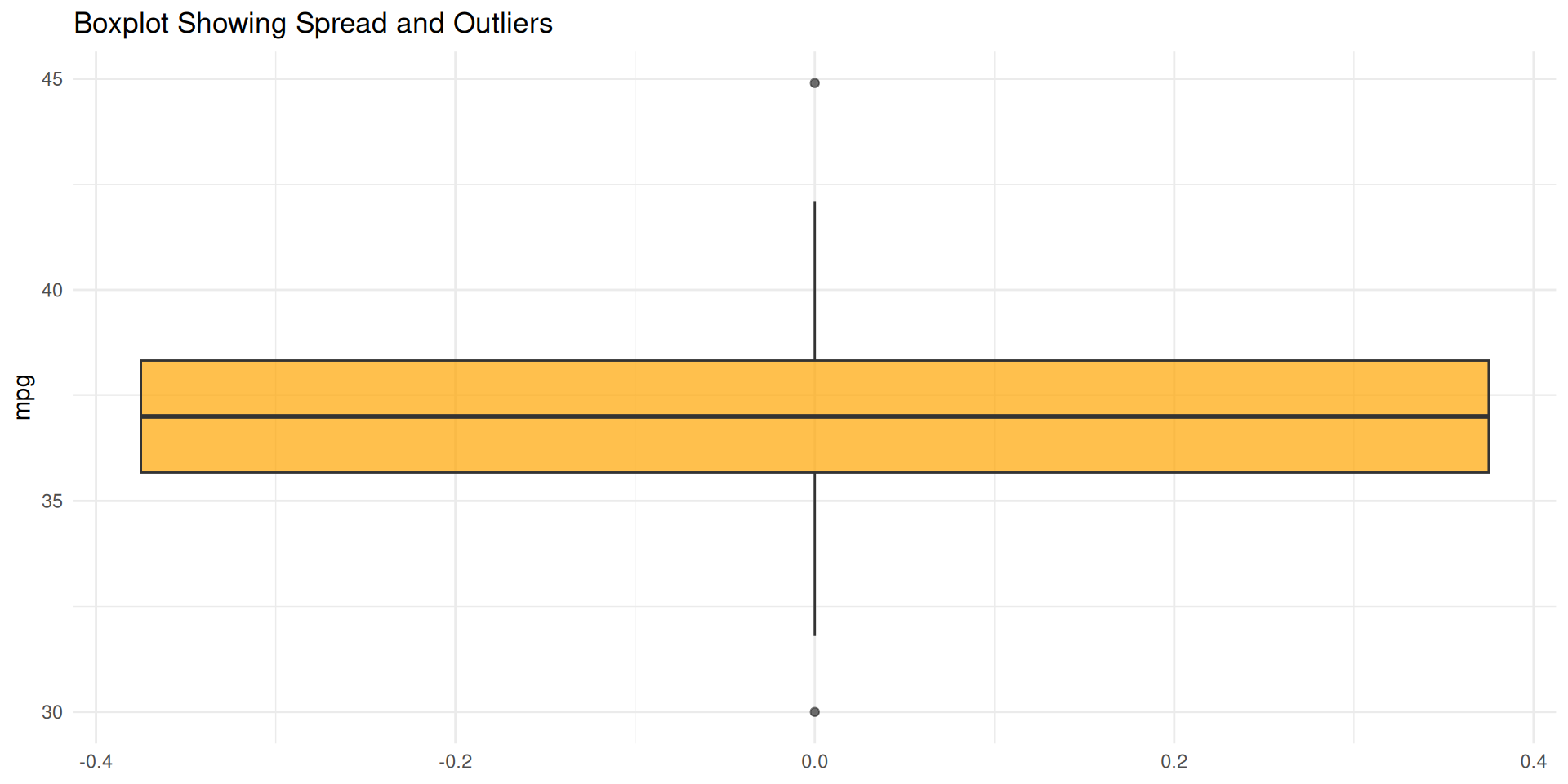
Boxplot: Outlier at 44.9 MPG waving red flag

Empirical Rule Check (Mixed Signals)

72% in μ±1σ (want 68%) → Close enough
95% in μ±2σ (perfect match) → Excellent
100% in μ±3σ (want 99.7%) → Slightly off

Quick Ratio Test (Confirmation)

IQR/SD = 1.1 (want 1.3) → Light tails detected

Verdict: Mildly non-normal → Consider transformations for critical analyses

Test Your Detective Skills!

Your Turn! Look at this histogram and Q-Q plot:

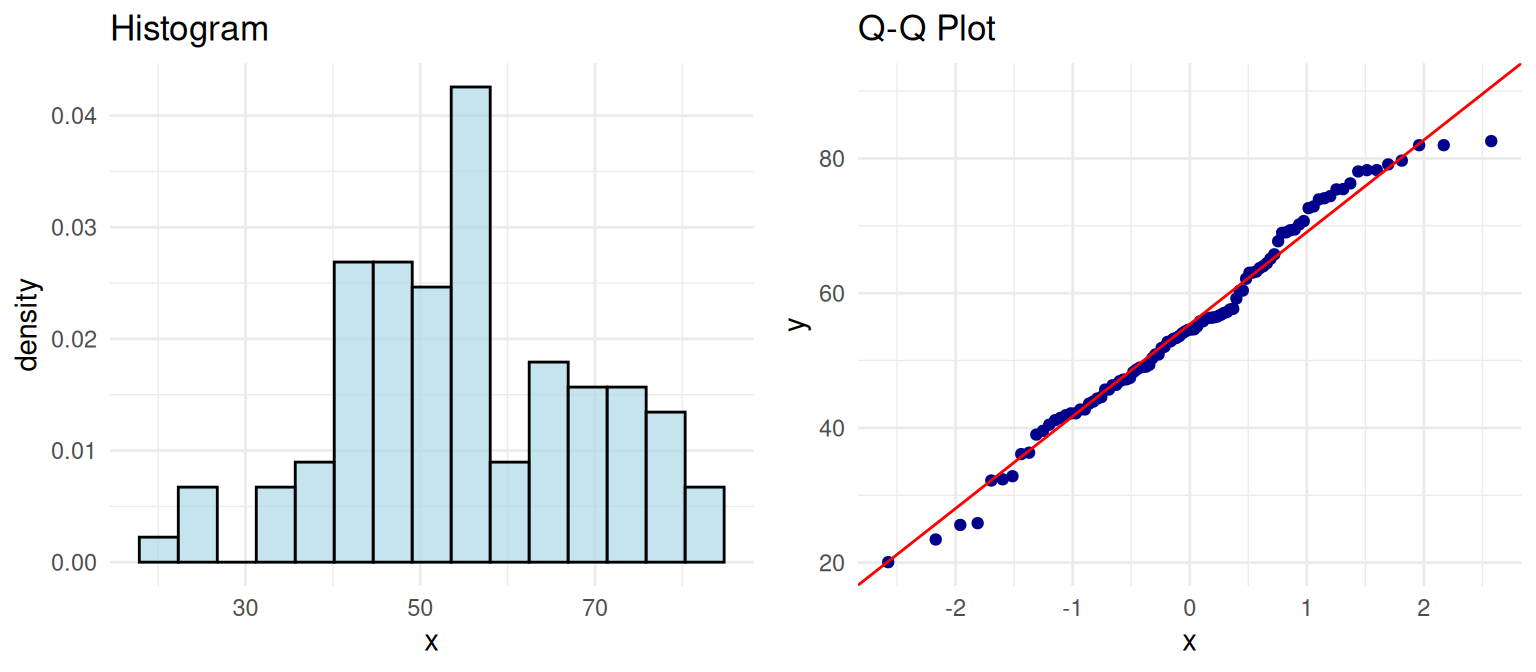
Question: Based on these plots, would you trust normal-based statistical tests for this data? Why or why not?

When Data Disappoints: The Transformation

The Problem: Your data isn’t normal → Normal-based tests are unreliable

The Solution: Transform the data to make it normal!

The Strategy: Try these transformations (in order):

Square Root: Mild right skew
Log: Moderate right skew
Box-Cox: Let software find the best one

Remember: Always check normality AFTER transforming!

Transformation Success Story

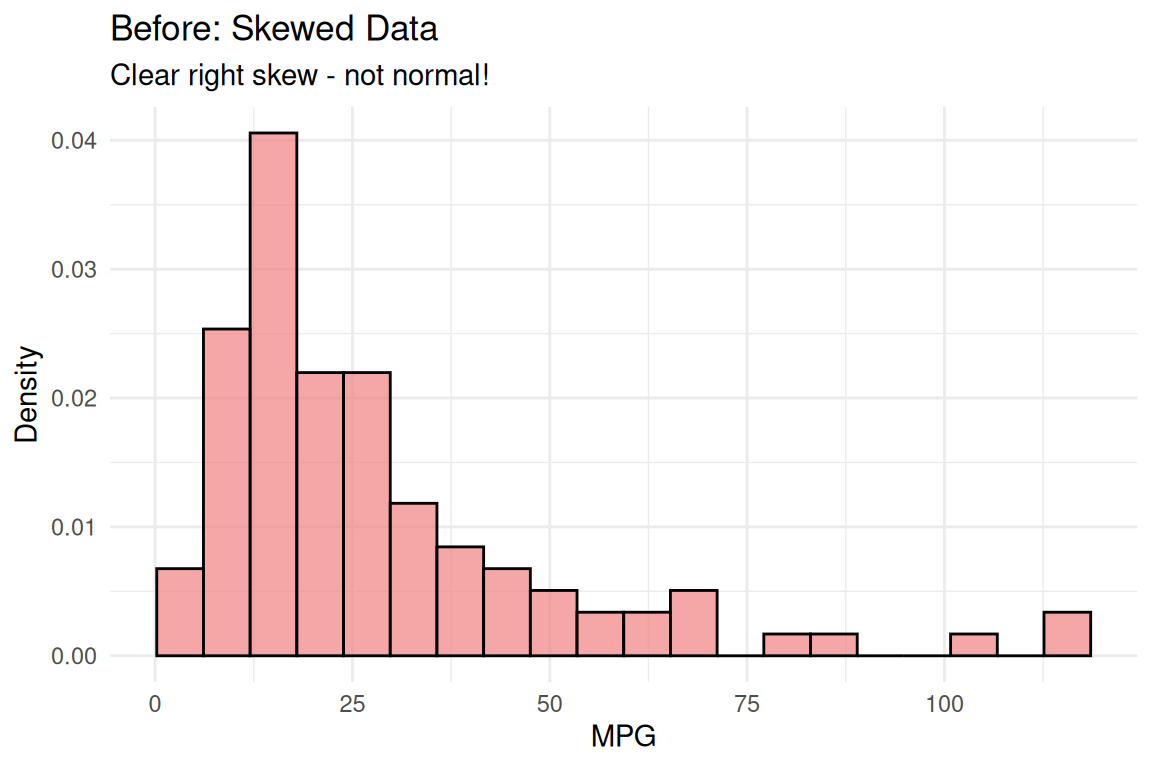
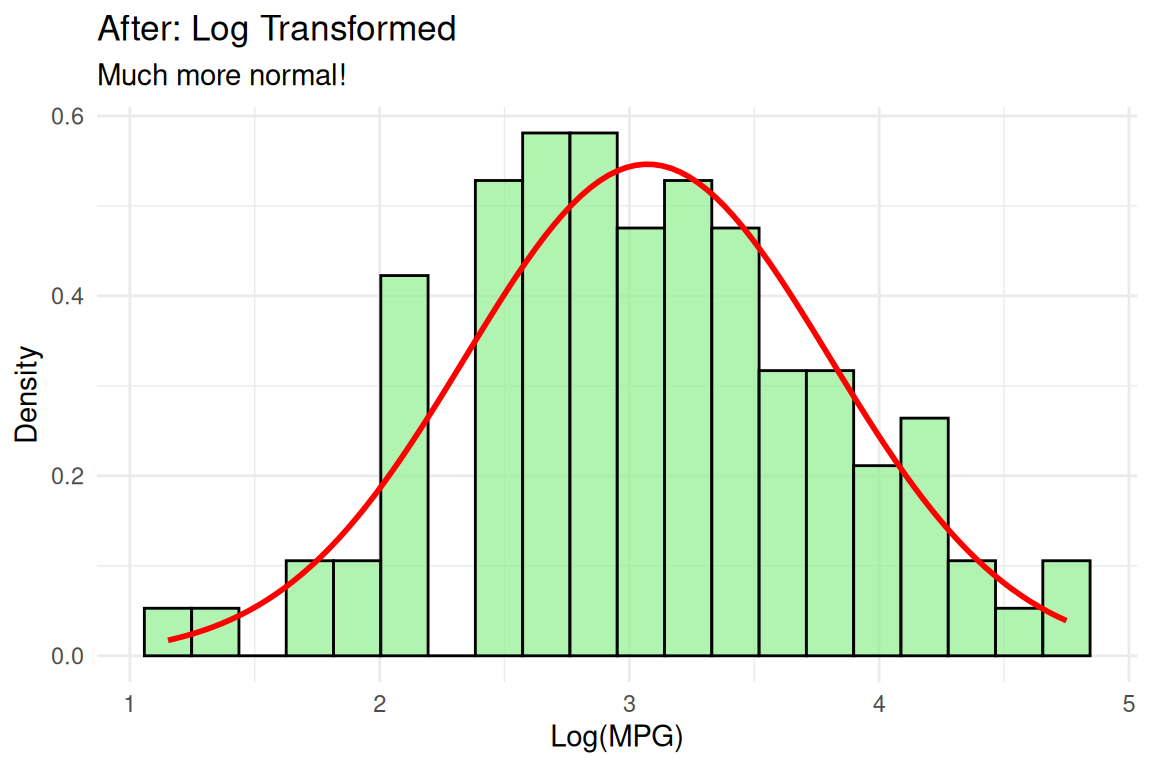
The Magic: Log transformation turned our skewed data into approximately normal data!

Result: Now we can safely use normal-based statistical tests on the transformed data.

Pro Tip: Always transform back to original scale for final interpretations.

Key Takeaways: Normality Toolkit

Master These Skills:

Visual Detection: Spot skewed tails and asymmetric patterns
3-Step Test: Quick normality assessment in under 2 minutes
Transformation Fix: Turn non-normal data into normal data

Quick Decision Rule:

Clearly Normal → Use normal-based tests confidently
Borderline/Unclear → Consider transformations or non-parametric alternatives
Clearly Non-Normal → Transform or use non-parametric methods