Day 17
Math 216: Statistical Thinking
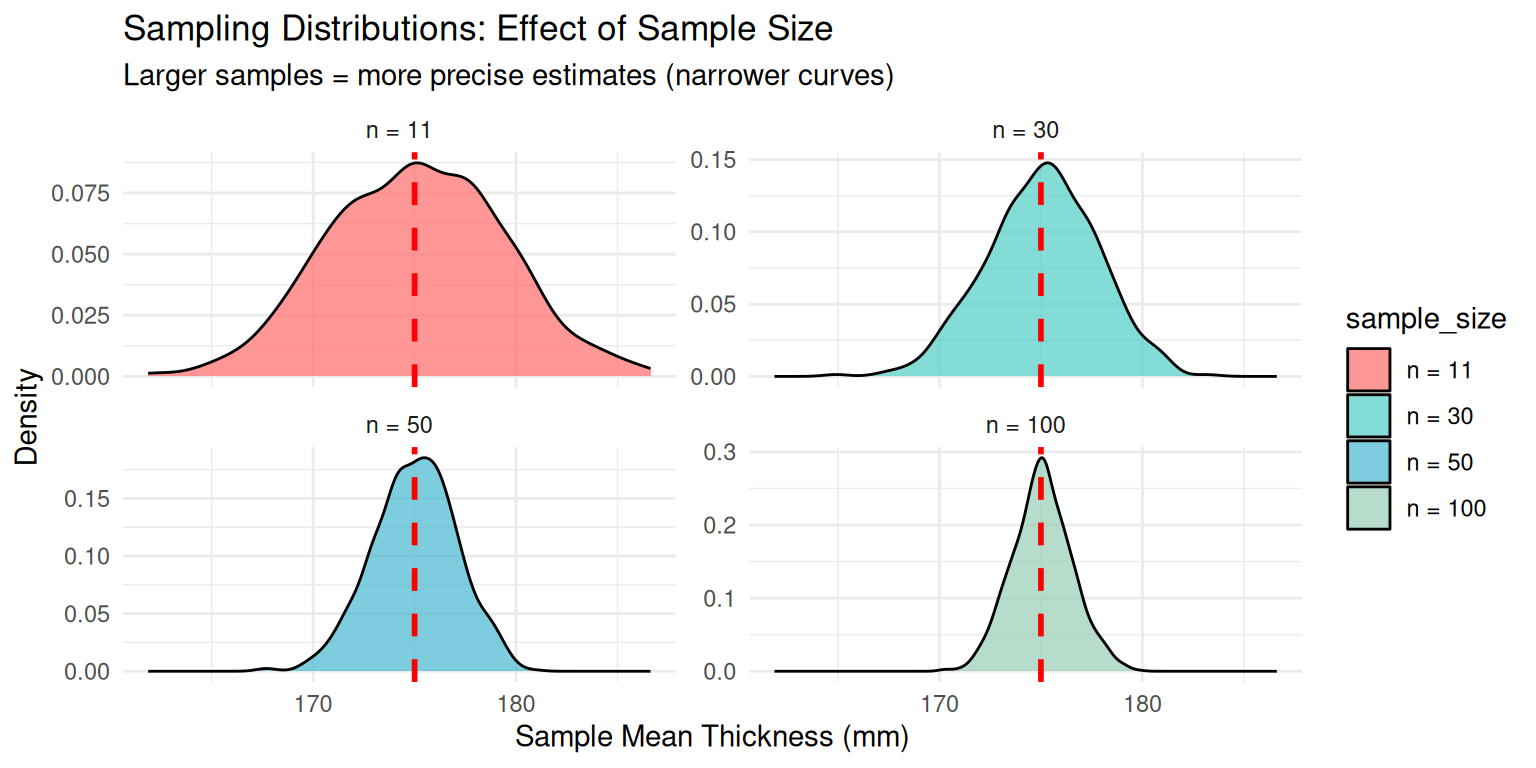
Central Limit Theorem: Foundation of Statistical Inference
Core Statistical Principle
Central Limit Theorem: For any population with finite mean μ and variance σ², the sampling distribution of the sample mean approaches a normal distribution as sample size increases.
Mathematical Formulation: \[\bar{x} \sim N\left(\mu, \frac{\sigma}{\sqrt{n}}\right)\]
Practical Significance: This universal principle enables statistical inference across diverse population distributions.
Case Study 1: Steel Manufacturing
Industrial Context: Steel sheets produced with uniform thickness distribution (150-200 mm). Quality assurance requires monitoring average thickness from small samples.
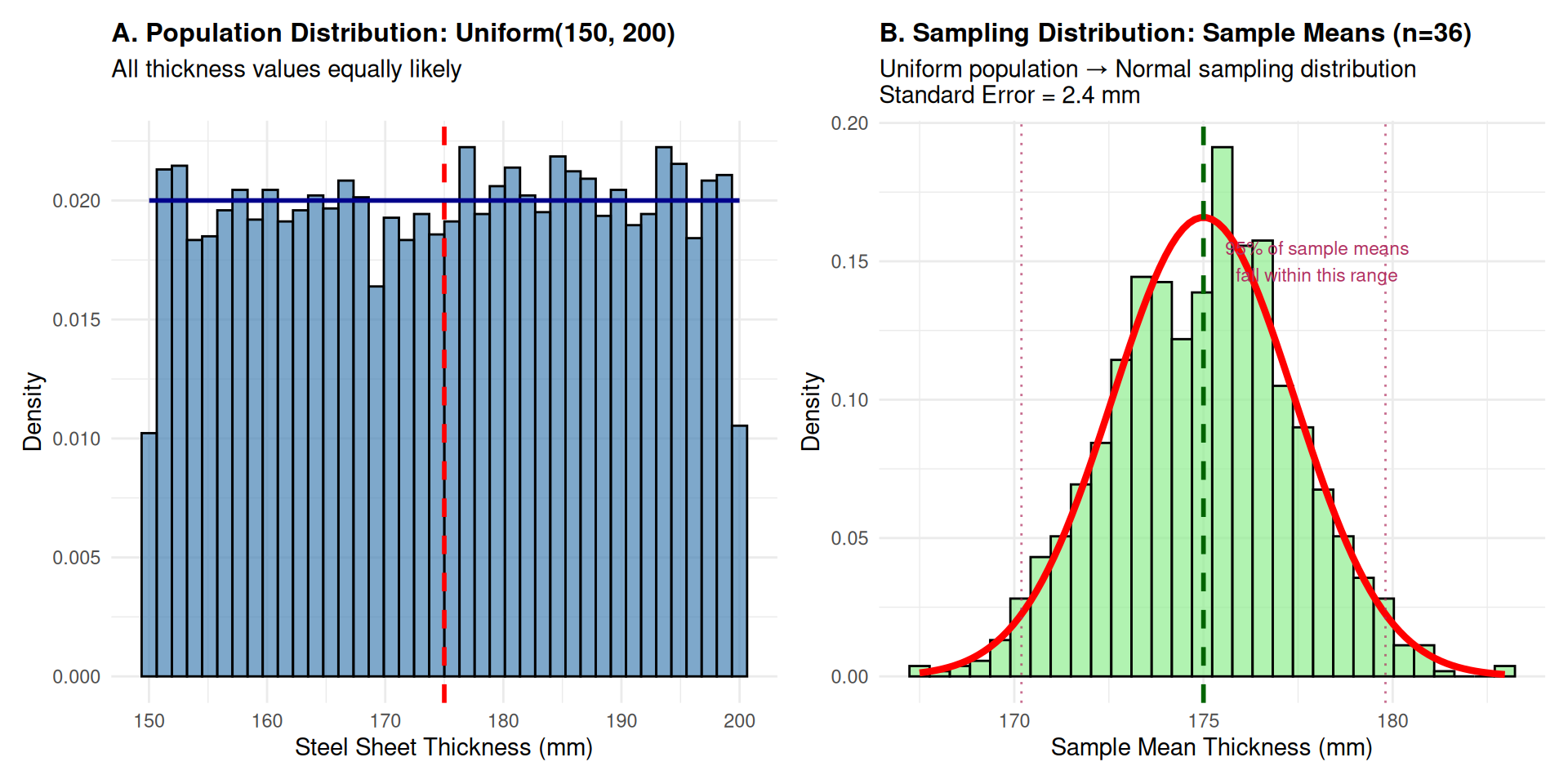
Case Study 1: Steel Manufacturing
Numerical Analysis Summary:
- Population Mean: 175.0 mm (theoretical)
- Population Standard Deviation: 14.43 mm (theoretical)
- Sample Size: 36 sheets per quality check
- Standard Error: 2.41 mm (σ/√n = 14.43/√36)
Statistical Insight: Despite uniform population distribution, sample means follow normal distribution with predictable precision!
Case Study 2: Exponential Distribution Analysis
Context: Customer service call durations follow exponential distribution with mean = 5 minutes.
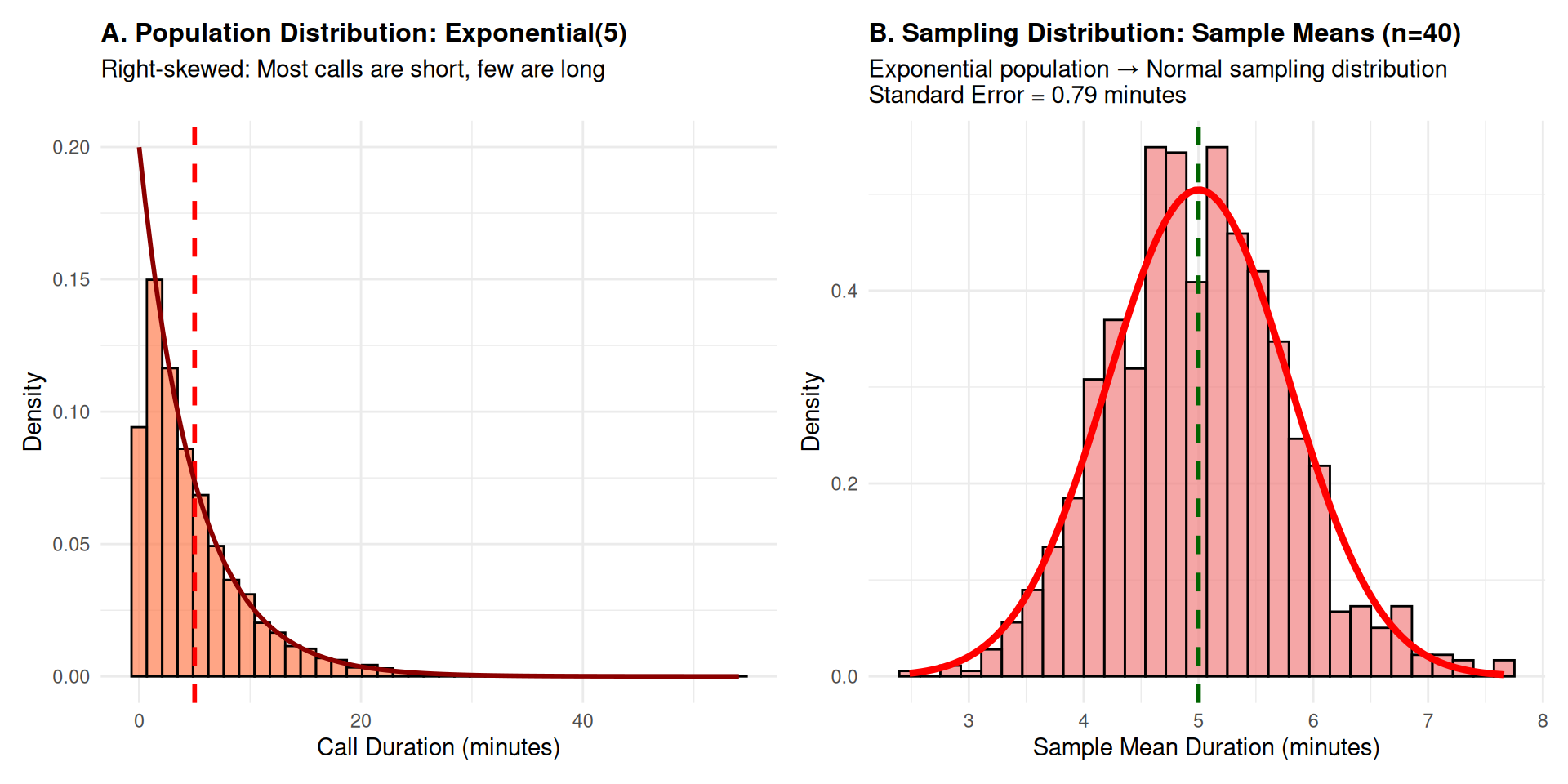
Statistical Insight: Even with highly skewed exponential population, sample means become normally distributed with n=40!
Case Study 3: Bimodal Distribution Analysis
Context: Product weights from two different production lines create bimodal distribution.
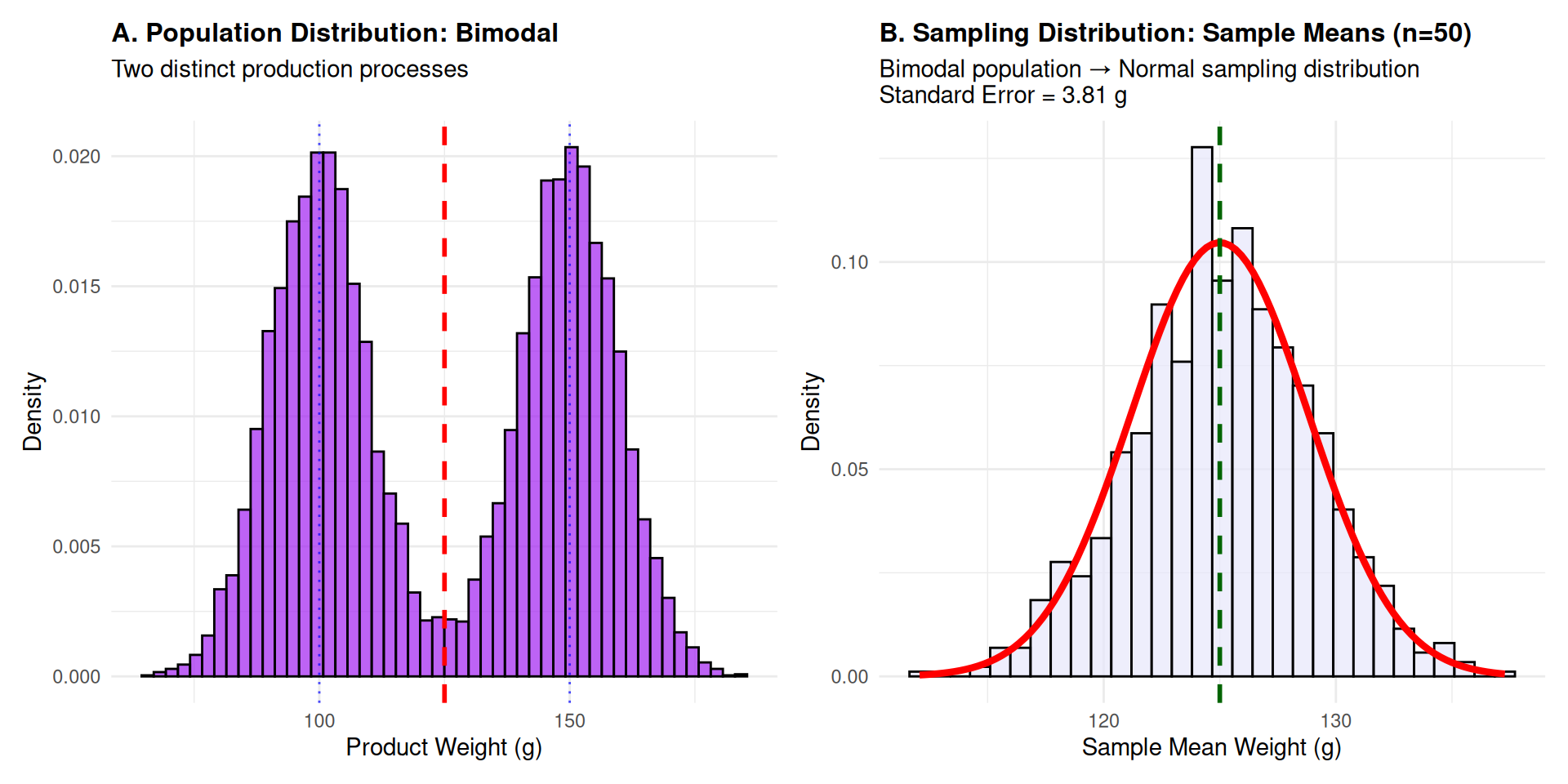
Statistical Insight: Complex bimodal populations still yield normally distributed sample means with adequate sample size!
Case Study 4: Left-Skewed Distribution Analysis
Context: Employee performance ratings with left-skewed distribution (most employees rated highly).
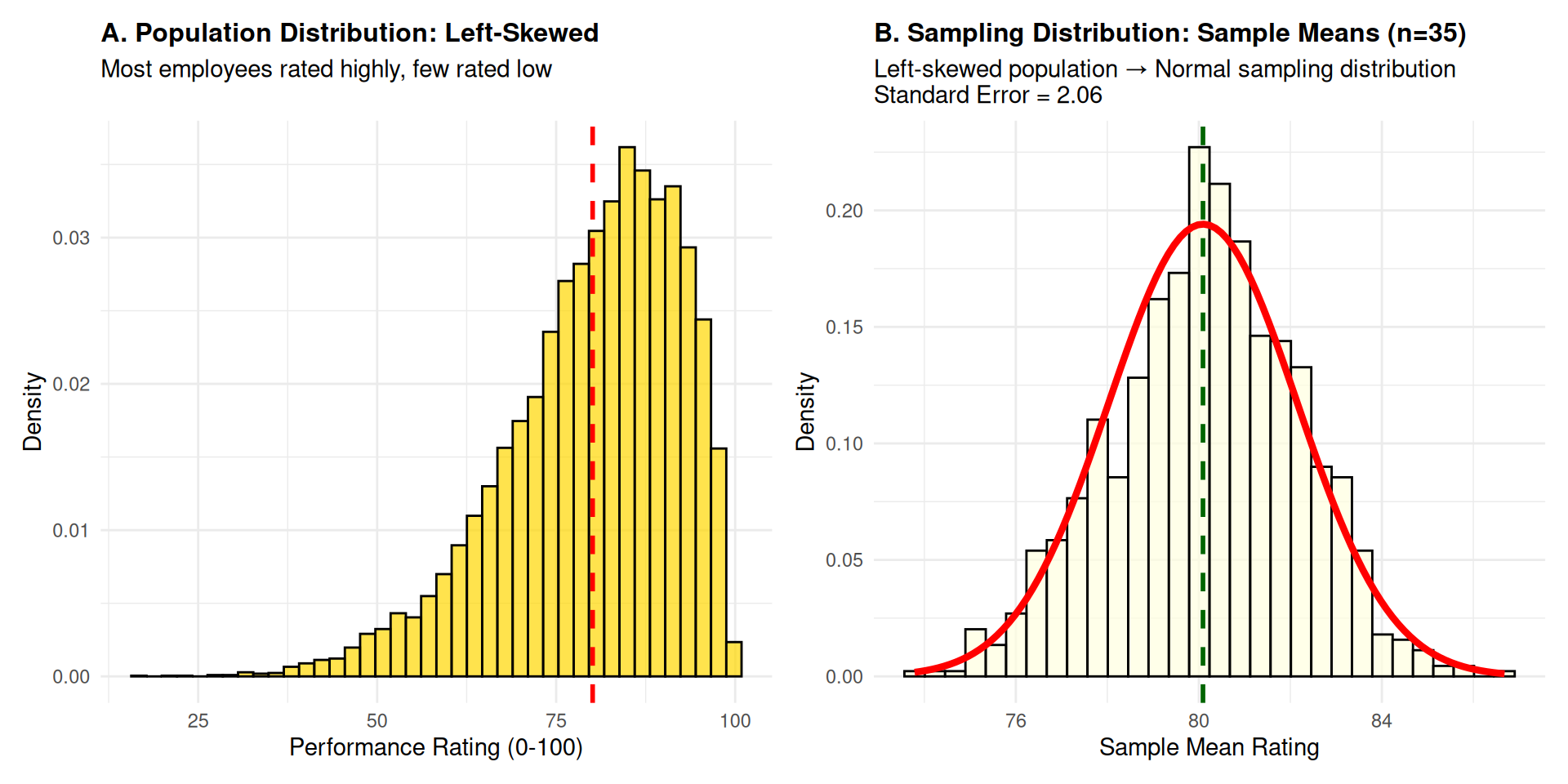
Statistical Insight: Left-skewed populations also produce normally distributed sample means with sufficient sample size!
Standard Error: Quantifying Estimation Precision
Standard Error Formula: \(SE = \frac{\sigma}{\sqrt{n}}\)
Applications of Central Limit Theorem: Political Polling
Context: Predicting election outcomes from voter samples
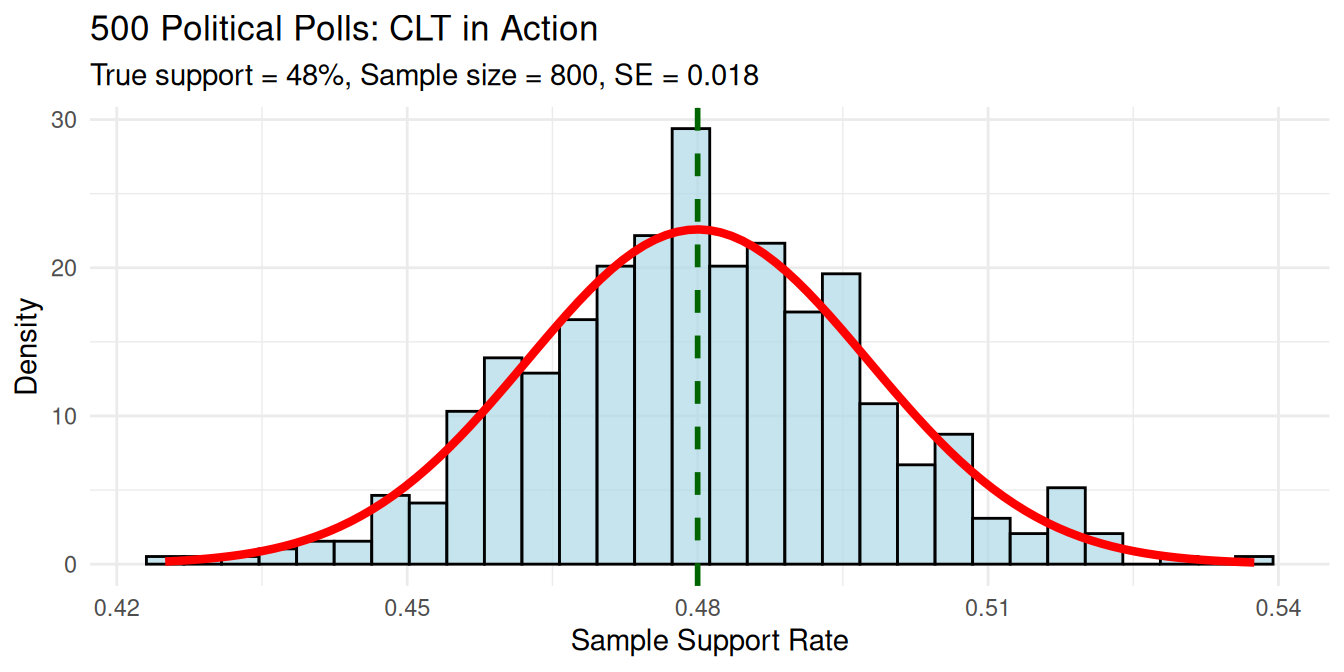
Statistical Findings:
- Poll results follow normal distribution despite binary data
- 95% of polls fall between 44.5% and 51.5%
- CLT enables accurate predictions from small samples
Applications of Central Limit Theorem: Quality Control
Context: Monitoring production quality from small samples
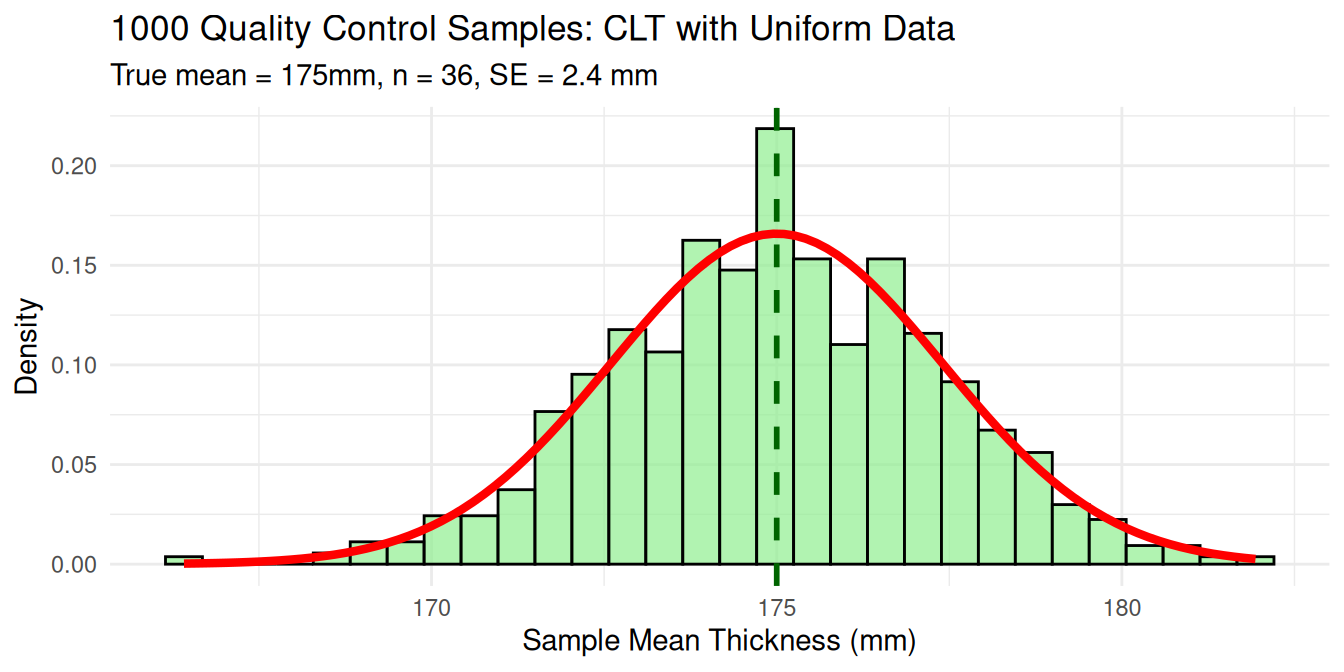
Quality Control Analysis:
- Uniform population → Normal sampling distribution
- 95% of samples fall within 174.3-175.7mm
- CLT works effectively with non-normal populations
Applications of Central Limit Theorem: Medical Research
Context: Testing drug effectiveness from clinical trials
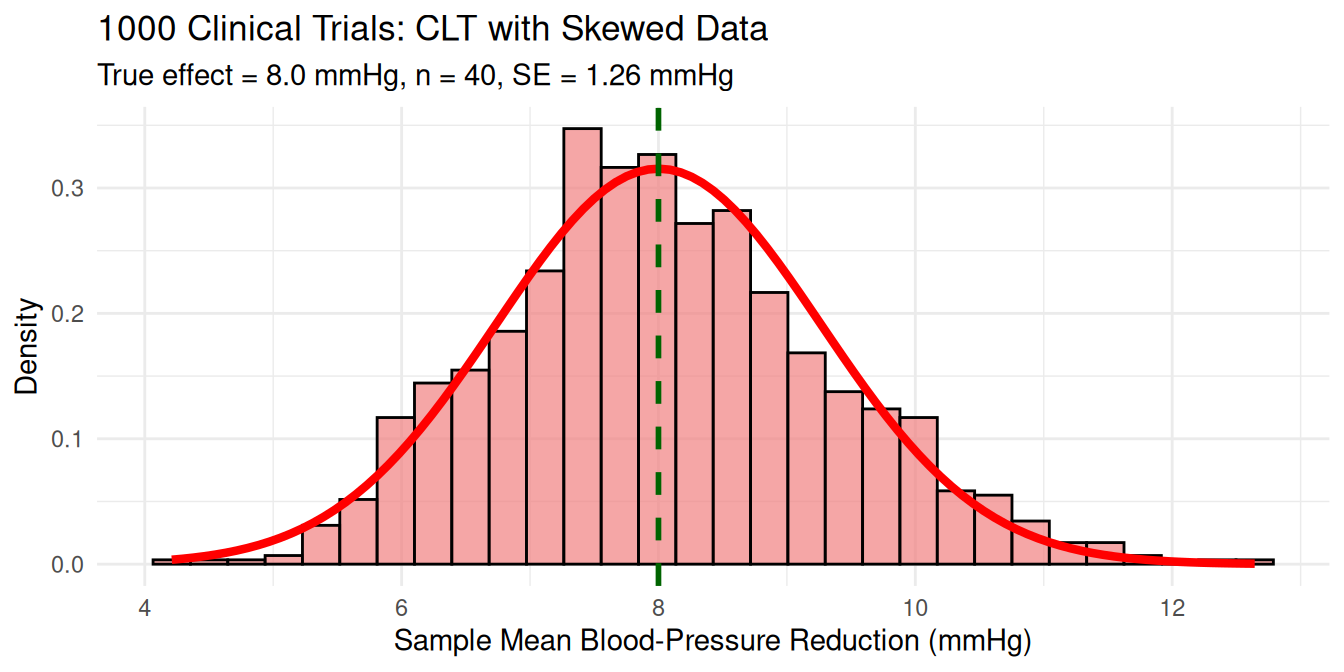
Medical Research Analysis:
- Skewed population → Normal sampling distribution
- CLT functions with any population shape
- Sample size is more critical than population distribution
Key Statistical Principles
Essential Statistical Concepts:
- Universal Normality: Sample means follow normal distribution regardless of population shape
- Precision Quantification: Standard error = σ/√n measures estimation accuracy
- Sample Size Effect: n ≥ 30 typically provides adequate CLT approximation
- Distribution Independence: Works with uniform, skewed, bimodal, and any finite-variance population
Statistical Guidelines:
- Sample size ≥ 30 → Sampling distribution is approximately normal
- Population shape → CLT works regardless of distribution
- Standard error → Quantifies precision of estimates
- Sample size increase → Improves estimation accuracy
Next Topic: Applying these principles to confidence intervals and hypothesis testing