Day 23
Math 216: Statistical Thinking
P-Values & Hypothesis Testing: From Evidence to Direction
How do we measure evidence against the null?
P-values quantify it—and the alternative hypothesis tells us which way to look!
Direction of the Alternative Sets the Rule
| Tail | \(H_a\) | P-value computes … |
|---|---|---|
| Right | \(\mu > \mu_0\) | probability in the upper tail |
| Left | \(\mu < \mu_0\) | probability in the lower tail |
| Two | \(\mu \neq \mu_0\) | probability in both tails |
Key: Pick \(H_a\) first; it governs the test direction and the P-value calculation.
Understanding P-Values
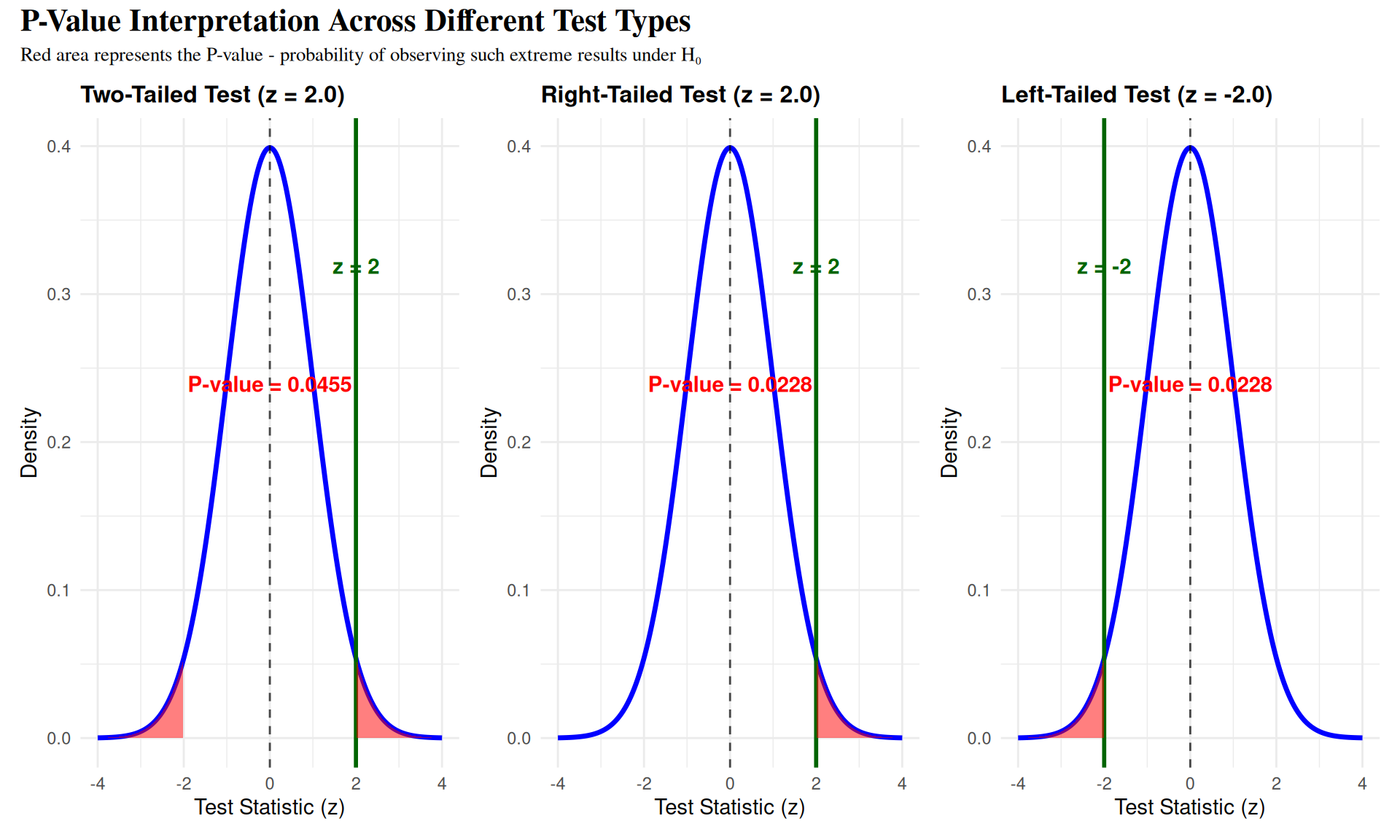
P-Value Definition and Interpretation
Core Statistical Concept
P-Value Definition:
- The \(p\)-value quantifies the level of disagreement between the sample data and the null hypothesis (\(H_0\))
- It is the probability, assuming \(H_0\) is true, of observing a test statistic as extreme as, or more extreme than, the statistic calculated from the sample data
Key Interpretations:
- Small P-value (\(p < 0.05\)): Strong evidence against \(H_0\)
- Large P-value (\(p > 0.05\)): Weak evidence against \(H_0\)
- Thresholds: 0.05 (significant), 0.01 (highly significant), 0.001 (very highly significant)
Statistical Insight: P-values measure the strength of evidence, not the probability that \(H_0\) is true!
P-Value Calculation Methods
P-Value Formulas by Test Type
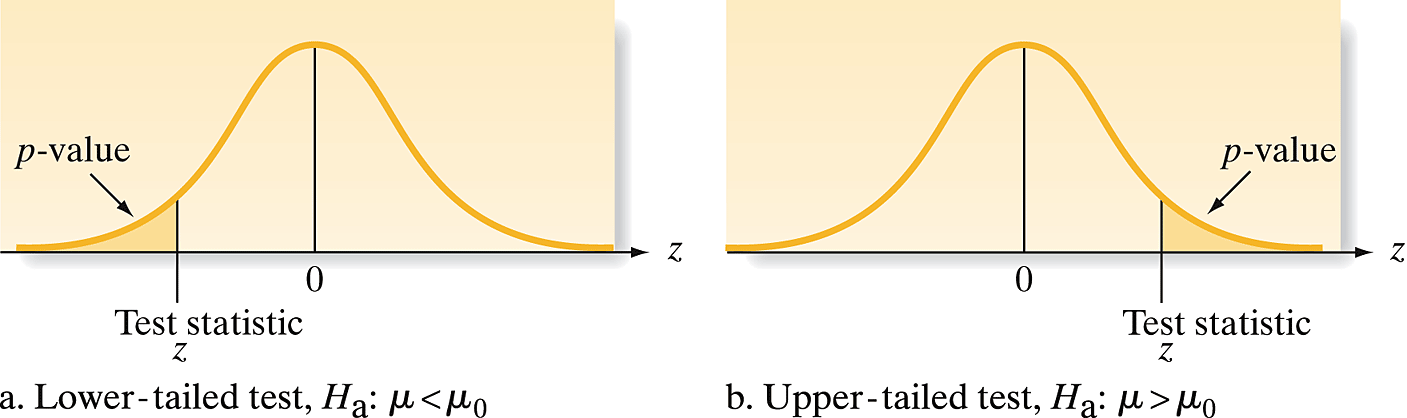
Right-Tailed Test: \[p = P(Z \geq z | H_0)\] - Example: Testing if new treatment is better than standard
Left-Tailed Test: \[p = P(Z \leq z | H_0)\] - Example: Testing if new process reduces defect rates
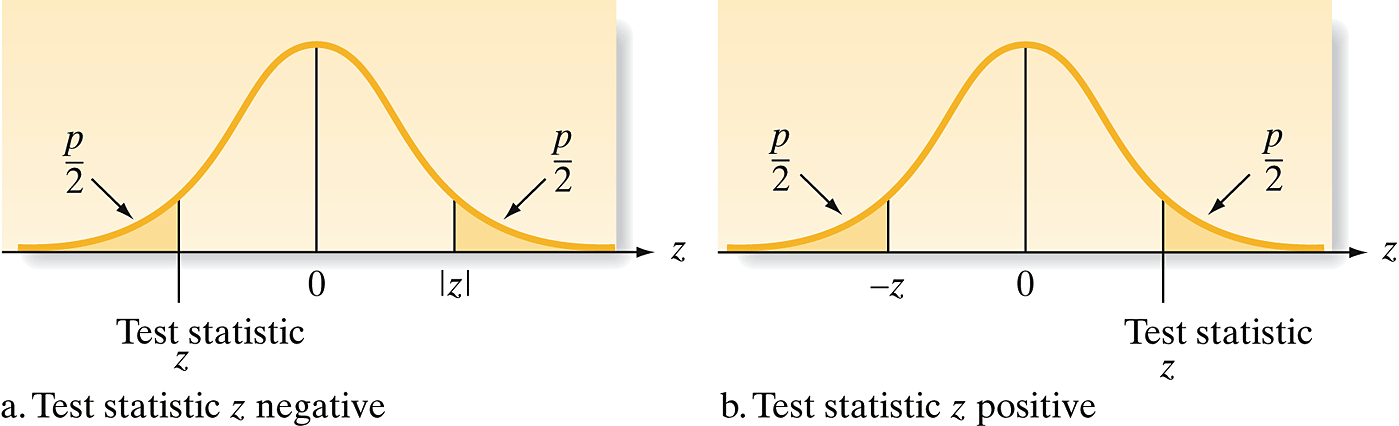
Two-Tailed Test: \[p = 2 \times P(Z \geq |z| | H_0)\] - Example: Testing if new method is different from current
R Implementation:
pnorm(z, lower.tail = FALSE)for right-tailedpnorm(z, lower.tail = TRUE)for left-tailed2 * pnorm(abs(z), lower.tail = FALSE)for two-tailed
Case Study 1: Medical Research P-Value Interpretation
Context: Clinical trial testing new drug effectiveness with sample data showing z = 2.3
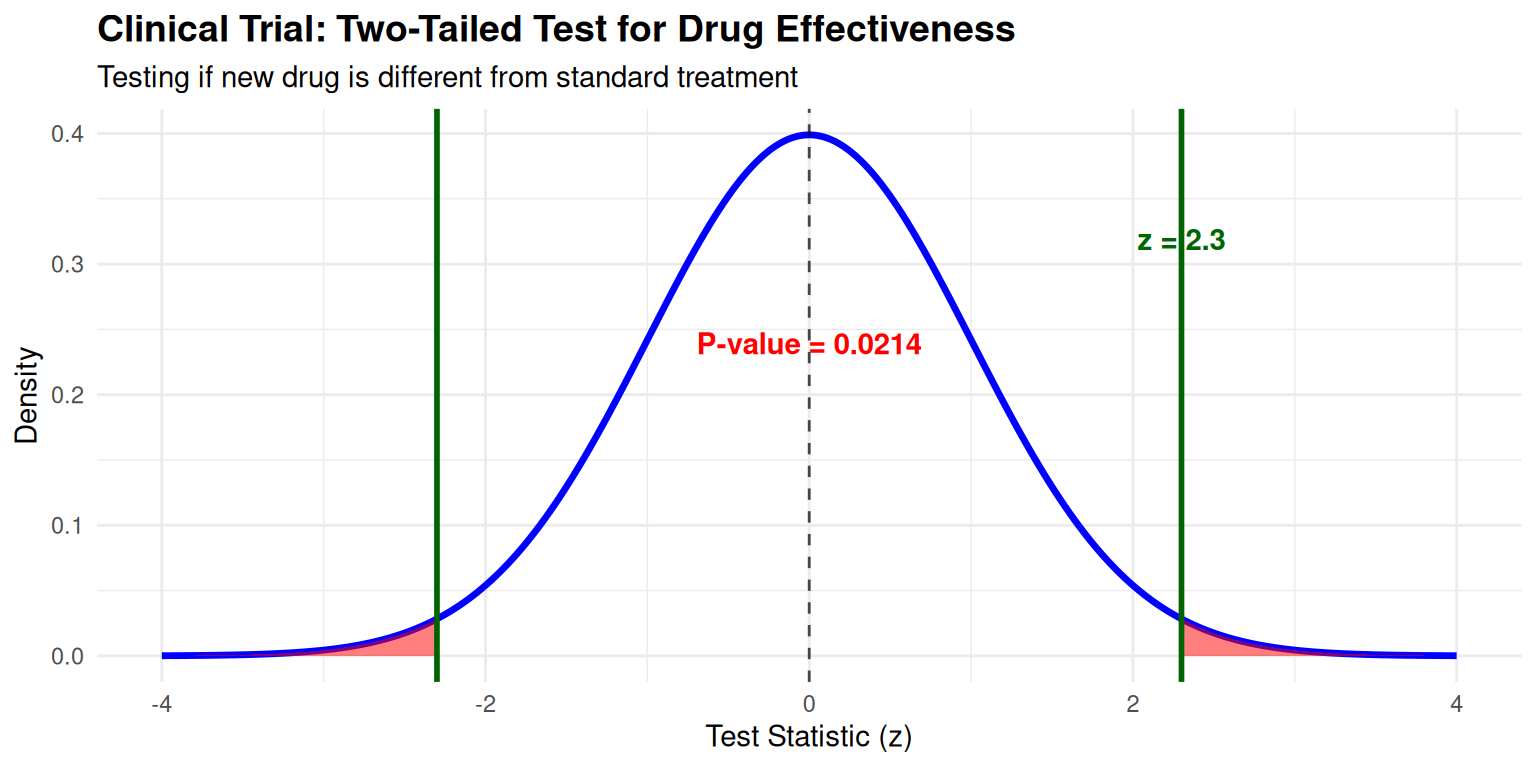
Statistical Analysis:
- P-value Calculation: \(p = 2 \times P(Z \geq |2.3|) = 2 \times (1 - P(Z \leq 2.3)) = 0.0214\)
- Interpretation: Strong evidence against null hypothesis (\(p < 0.05\))
- Conclusion: Statistically significant evidence that the new drug differs from standard treatment
Case Study 2: Quality Control P-Value Application
Context: Manufacturing process improvement testing with z = -2.8
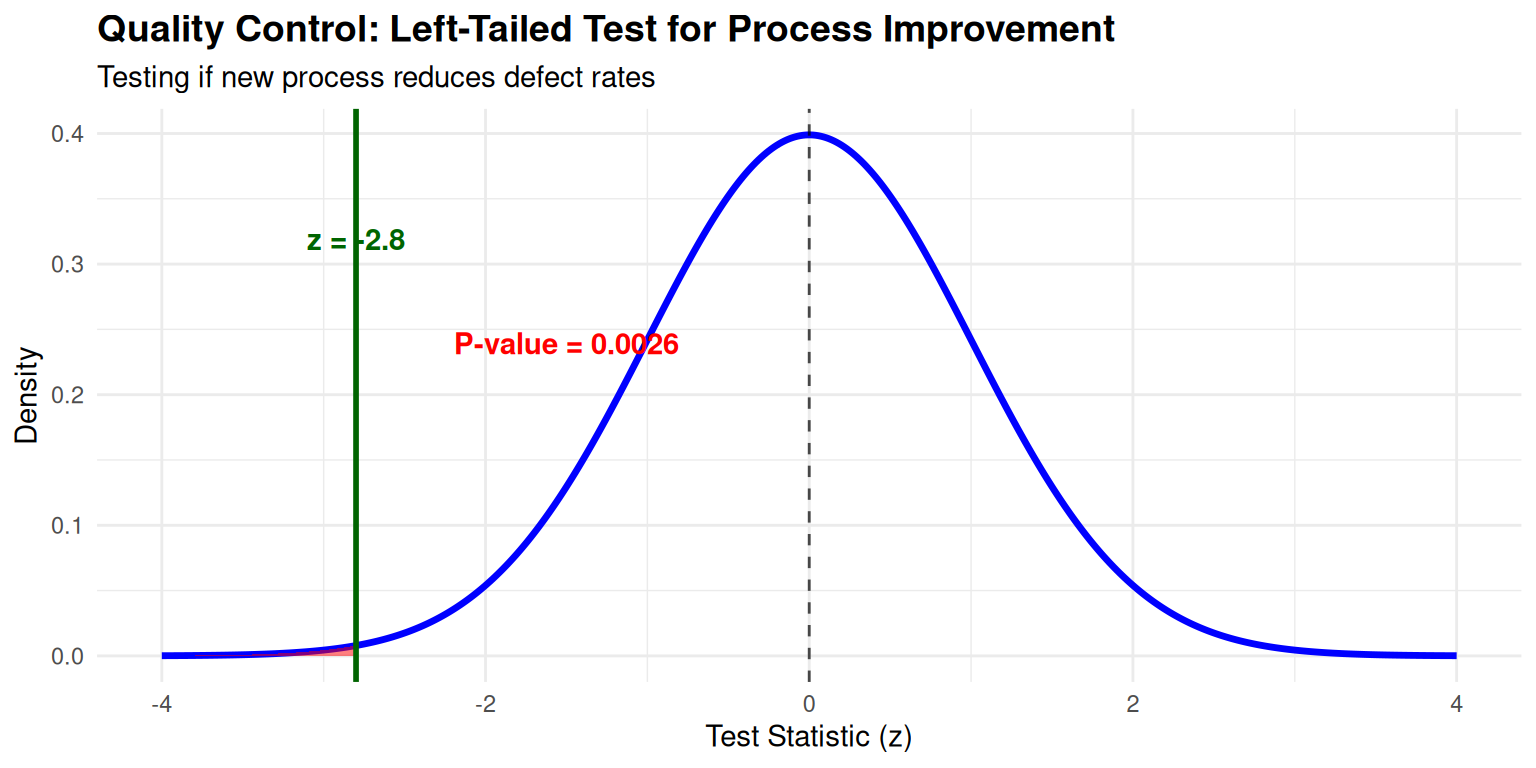
Statistical Analysis:
- P-value Calculation: \(p = P(Z \leq -2.8) = 0.0026\)
- Interpretation: Very strong evidence against null hypothesis (\(p < 0.01\))
- Conclusion: Highly significant evidence that the new process reduces defect rates
P-Value Calculation Exercises
Practical P-Value Calculations Using R
Exercise 1: Two-Tailed Test P-Value
- Test statistic: z = 1.96
- P-value calculation:
2 * pnorm(1.96, lower.tail = FALSE) - Result: p = 0.05 (exactly at significance threshold)
- Interpretation: Marginal evidence against null hypothesis
Exercise 2: Right-Tailed Test P-Value
- Test statistic: z = 2.5
- P-value calculation:
pnorm(2.5, lower.tail = FALSE) - Result: p = 0.0062
- Interpretation: Strong evidence against null hypothesis
P-Value Calculation Exercises
Practical P-Value Calculations Using R
Exercise 3: Left-Tailed Test P-Value
- Test statistic: z = -1.75
- P-value calculation:
pnorm(-1.75, lower.tail = TRUE) - Result: p = 0.0401
- Interpretation: Evidence against null hypothesis at 5% level
Exercise 4: Real-World Interpretation
- Market research: z = 2.1, p = 0.0357
- Interpretation: Statistically significant evidence of consumer preference change
- Business decision: Strong evidence to support marketing strategy change
Key Statistical Principles
Essential P-Value Concepts:
- Evidence Quantification: P-values measure strength of evidence against null hypothesis
- Statistical Significance: Thresholds (0.05, 0.01, 0.001) provide decision criteria
- Test Type Selection: Right-tailed, left-tailed, or two-tailed based on research question
- Interpretation Framework: Focus on evidence strength, not absolute certainty
Statistical Guidelines:
- Significance Level: Choose appropriate α level for research context
- Test Direction: Match test type to alternative hypothesis
- Evidence Interpretation: Small P-values indicate strong evidence against H₀
- Practical Significance: Consider both statistical and practical importance
Common P-Value Misinterpretations
- NOT: Probability that H₀ is true
- NOT: Probability that Hₐ is false
- NOT: Measure of effect size
- NOT: Probability of Type I error for specific test
Next Topic: Extending P-value framework to different types of hypothesis tests