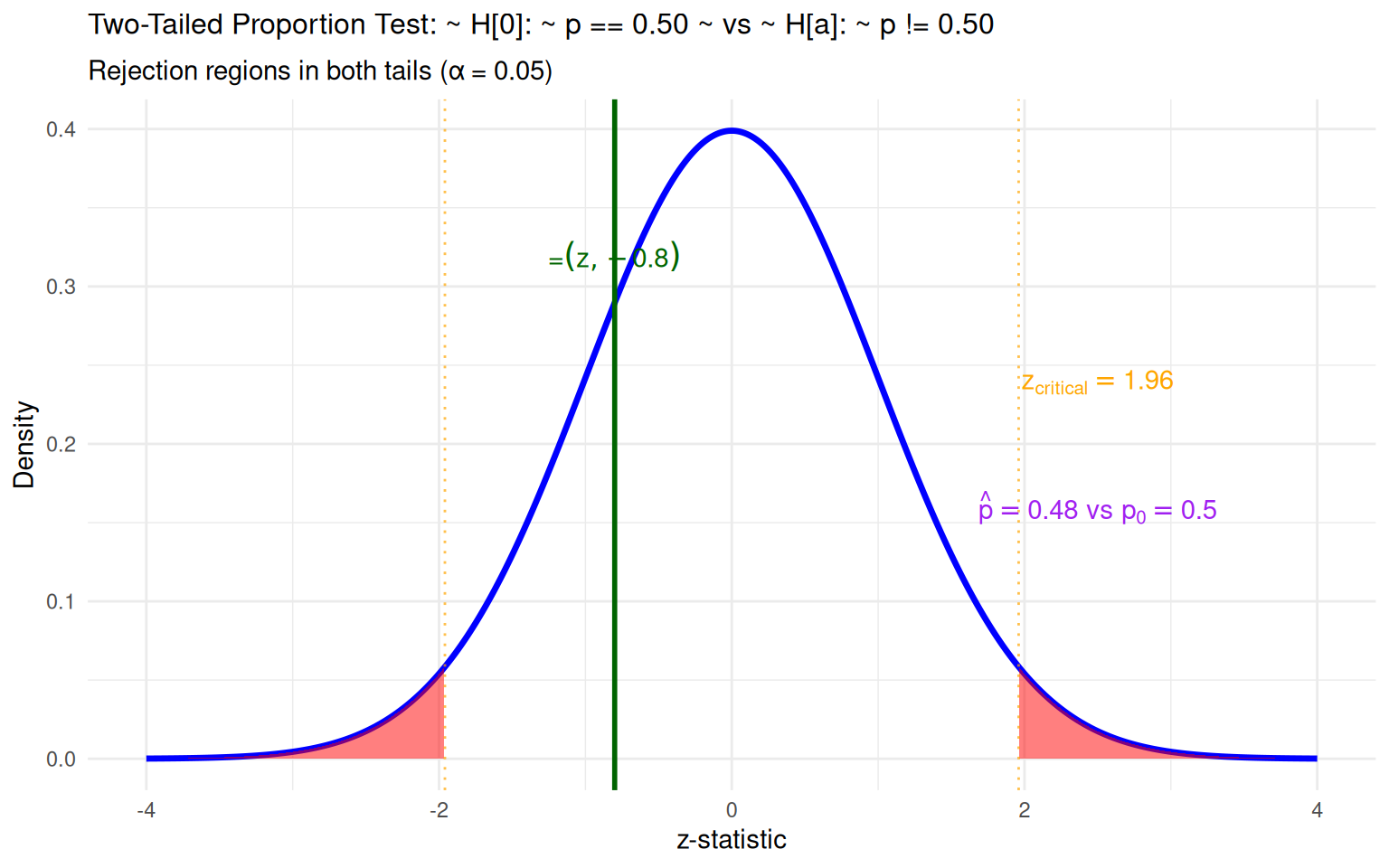
# Two-tailed proportion test
prop.test(x = 192, n = 400, p = 0.50, alternative = "two.sided", correct = FALSE)
1-sample proportions test without continuity correction
data: 192 out of 400
X-squared = 0.64, df = 1, p-value = 0.4237
alternative hypothesis: true p is not equal to 0.5
95 percent confidence interval:
0.4314634 0.5289171
sample estimates:
p
0.48