Day 34

Math 216: Statistical Thinking

Bastola

Chi-Square Test of Independence

Key Question: Are two categorical variables related, or are they independent?

  • When to Use: Testing association between two categorical variables

  • Real-World Applications:

    • Does vaccination status affect flu contraction?
    • Is political affiliation related to policy preferences?
    • Are smoking habits associated with lung disease?

Core Concept: Compare observed joint frequencies with expected frequencies under independence

Contingency Tables: The Foundation

Understanding Two-Way Tables:

Column 1 Column 2 … Column c Total
Row 1 \(n_{11}\) \(n_{12}\) … \(n_{1c}\) \(r_1\)
Row 2 \(n_{21}\) \(n_{22}\) … \(n_{2c}\) \(r_2\)
… \(\vdots\) \(\vdots\) … \(\vdots\) \(\vdots\)
Row r \(n_{r1}\) \(n_{r2}\) … \(n_{rc}\) \(r_r\)
Total \(c_1\) \(c_2\) … \(c_c\) \(n\)

Where:

  • \(n_{ij}\) = Observed count in cell (i,j)
  • \(r_i\) = Row total for row i
  • \(c_j\) = Column total for column j
  • \(n\) = Grand total

Key Insight: If variables are independent, cell frequencies should follow row × column proportions

Test of Independence Framework

flowchart LR
    %% Styling definitions
    classDef start fill:#FFFACD,stroke:#FF8C00,stroke-width:2px,color:#000
    classDef decision fill:#E6F3FF,stroke:#1E88E5,stroke-width:2px,color:#000
    classDef action fill:#E8F5E9,stroke:#43A047,stroke-width:2px,color:#000
    classDef endStyle fill:#FFEBEE,stroke:#E53935,stroke-width:2px,color:#000

    %% Nodes
    %% Text wrapped to be tall/narrow to save horizontal space
    A(["Start:<br/>Contingency<br/>Table"]):::start
    B{"State H₀:<br/>Variables<br/>Indep."}:::decision
    C{"Calculate<br/>Expected<br/>Counts"}:::decision
    D{"Compute<br/>χ² Statistic"}:::decision
    E{"Compare to<br/>χ² Dist."}:::decision
    F["Reject H₀<br/>Evidence of<br/>Relationship"]:::action
    G["Fail to<br/>Reject H₀<br/>No Evidence"]:::action
    H["Interpret<br/>Association"]:::endStyle

    %% Flow connections
    A --> B
    B --> C
    C --> D
    D --> E
    E -->|p < α| F
    E -->|p ≥ α| G
    F --> H
    G --> H
Figure 1: Chi-Square Test of Independence Flowchart

The Chi-Square Test Statistic

How We Measure Association:

\[\chi^2 = \sum_{i=1}^{r} \sum_{j=1}^{c} \frac{(O_{ij} - E_{ij})^2}{E_{ij}}\]

Where:

  • \(O_{ij}\) = Observed count in cell (i,j)
  • \(E_{ij}\) = Expected count under independence
  • \(E_{ij} = \frac{r_i \times c_j}{n}\)

Degrees of Freedom: \[ df = (r - 1) \times (c - 1) \]

Intuition: Large \(\chi^2\) values indicate strong association between variables

Example 1: Flu Vaccine Effectiveness

Research Question: Does flu vaccination reduce flu contraction?

Data: 1000 individuals surveyed

Status No Vaccine One Shot Two Shot Total
Flu 24 9 13 46
No Flu 289 100 565 954
Total 313 109 578 1000

Hypotheses:

  • \(H_0\): Flu status and vaccination status are independent
  • \(H_a\): Flu status and vaccination status are dependent

Expected: If independent, flu rates should be similar across vaccination groups

Vaccine Effectiveness Test: R Implementation

# Create contingency table for vaccine data
flu_vaccine_data <- matrix(c(24, 9, 13, 289, 100, 565),
                          nrow = 2, byrow = TRUE,
                          dimnames = list(c("Flu", "No Flu"),
                                         c("No Vaccine", "One Shot", "Two Shot")))

# Perform chi-square test
vaccine_test <- chisq.test(flu_vaccine_data, correct = FALSE)
vaccine_test

    Pearson's Chi-squared test

data:  flu_vaccine_data
X-squared = 17.313, df = 2, p-value = 0.000174

Detailed Results:
Chi-square statistic = 17.313 
Degrees of freedom = 2 
P-value = 1.739948e-04 
Expected counts under independence:
       No Vaccine One Shot Two Shot
Flu          14.4     5.01    26.59
No Flu      298.6   103.99   551.41

Decision: REJECT H₀ (p < 0.05)
Conclusion: Evidence that vaccination affects flu contraction

Visualizing Vaccine Effectiveness

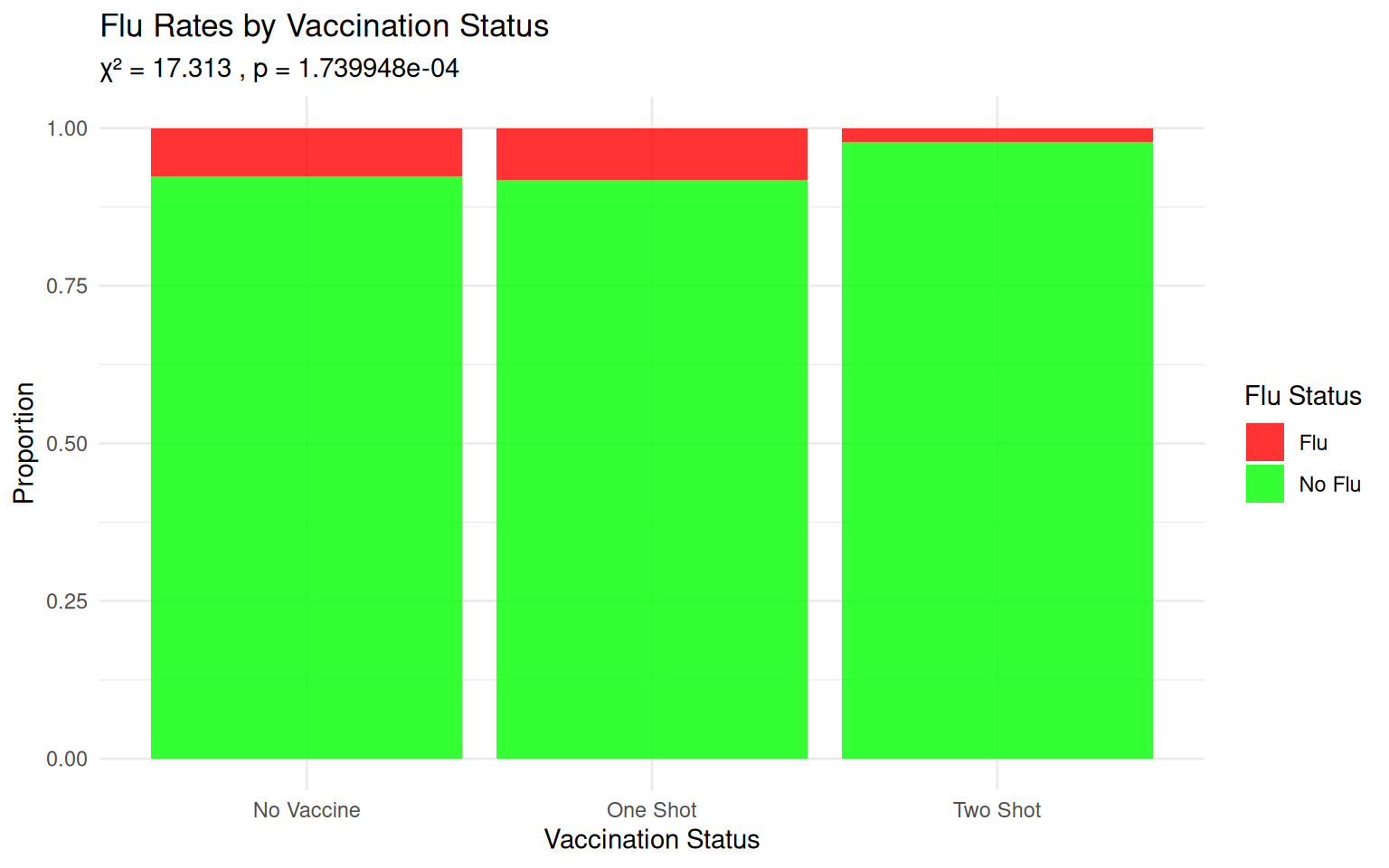
Example 2: Political Views & Space Exploration

Research Question: Is political affiliation related to support for space exploration?

Data: 100 individuals surveyed

Support Level Republican Democrat Independent Total
Strong 8 10 12 30
Moderate 12 17 6 35
Weak 10 13 12 35
Total 30 40 30 100

Hypotheses:

  • \(H_0\): Political affiliation and space support are independent
  • \(H_a\): Political affiliation and space support are dependent

Expected: If independent, support patterns should be similar across political groups

Political Views Test: R Implementation

# Create contingency table for political views
politics_data <- matrix(c(8, 10, 12, 12, 17, 6, 10, 13, 12),
                       nrow = 3, byrow = TRUE,
                       dimnames = list(c("Strong", "Moderate", "Weak"),
                                      c("Republican", "Democrat", "Independent")))

# Perform chi-square test
politics_test <- chisq.test(politics_data, correct = FALSE)
politics_test

    Pearson's Chi-squared test

data:  politics_data
X-squared = 4.5397, df = 4, p-value = 0.3379

Detailed Results:
Chi-square statistic = 4.54 
Degrees of freedom = 4 
P-value = 0.3379 
Expected counts under independence:
         Republican Democrat Independent
Strong          9.0       12         9.0
Moderate       10.5       14        10.5
Weak           10.5       14        10.5

Decision: FAIL TO REJECT H₀ (p ≥ 0.05)
Conclusion: No evidence of relationship between politics and space support

Visualizing Political Views Data

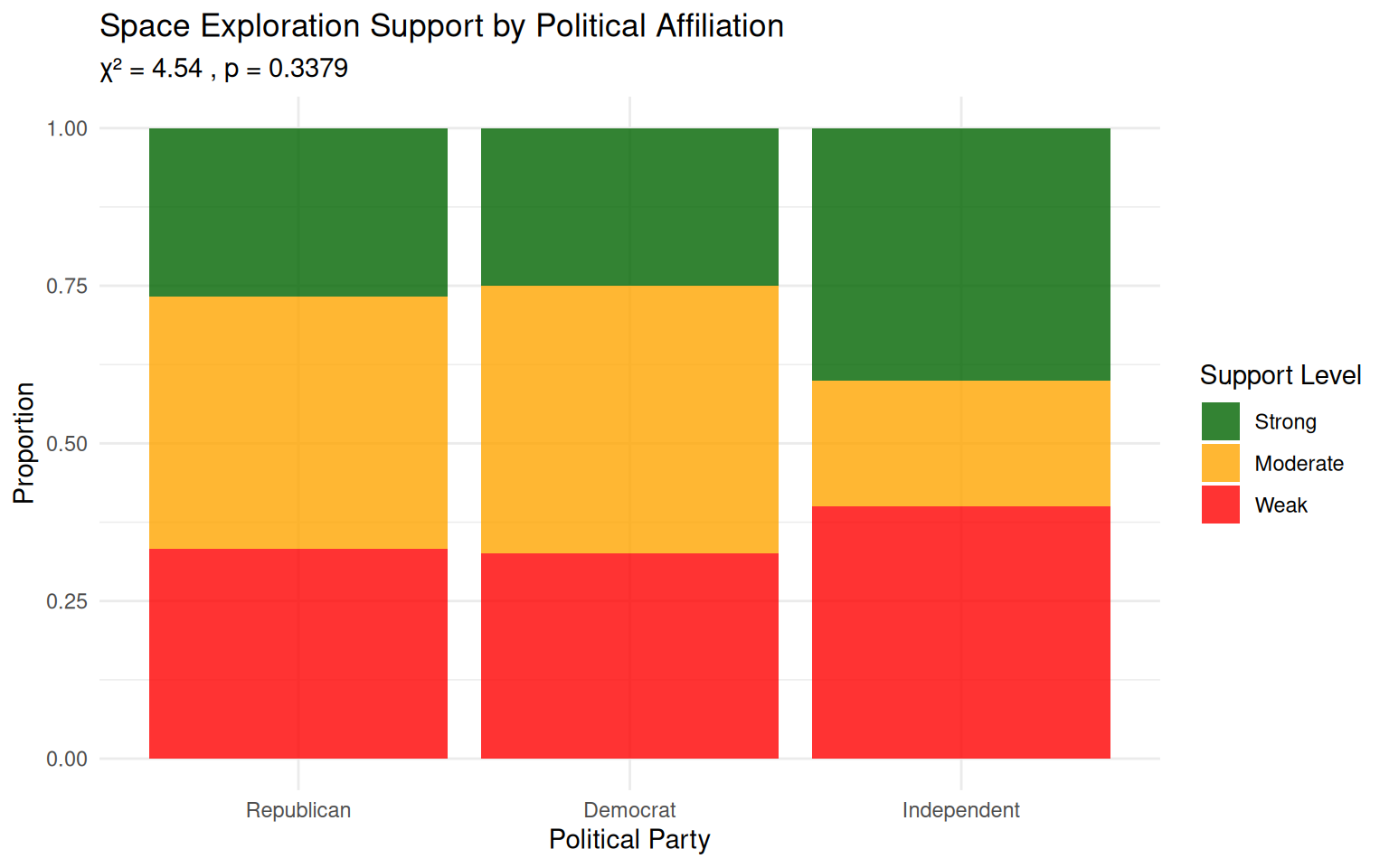
Test of Independence Assumptions

Critical Requirements for Valid Testing:

  1. Independence: Observations must be independent of each other
  2. Sample Size: All expected counts should be ≥ 5
  3. Categorical Data: Both variables must be categorical
  4. Random Sampling: Data should come from random sampling

When Assumptions Fail:

  • Small expected counts → Use Fisher’s exact test
  • Continuous variables → Use correlation or regression

Rule of Thumb: If >20% of cells have \(E_{ij} < 5\), consider combining categories

Test of Independence Summary

Your Testing Checklist:

  1. State Hypotheses: \(H_0\): independence vs \(H_a\): dependence
  2. Calculate Expected: \(E_{ij} = \frac{r_i \times c_j}{n}\)
  3. Compute Test Statistic: \(\chi^2 = \sum \frac{(O_{ij} - E_{ij})^2}{E_{ij}}\)
  4. Determine Degrees of Freedom: \(df = (r-1)(c-1)\)
  5. Find P-value: Compare \(\chi^2\) to chi-square distribution
  6. Make Decision: Reject \(H_0\) if p-value < α
  7. Interpret Results: Practical significance and effect size

Key Insight: Chi-square tests reveal whether patterns in contingency tables reflect real relationships!

R Toolkit: Chi-Square Test of Independence

Basic Chi-Square Test

# Test independence in contingency table
chisq.test(contingency_table, correct = FALSE)

Creating Contingency Tables

# From matrix
my_table <- matrix(c(10, 20, 30, 40), nrow = 2)

# From data frame using table()
my_table <- table(data$var1, data$var2)

# From data frame using xtabs()
my_table <- xtabs(~ var1 + var2, data = data)

Extracting Results

# Get test components
test_result$statistic    # Chi-square value
test_result$p.value      # P-value
test_result$parameter    # Degrees of freedom
test_result$expected     # Expected counts
test_result$observed     # Observed counts

Goodness of Fit vs Test of Independence

Key Differences:

Aspect Goodness of Fit Test of Independence
Purpose Test if data fits specified distribution Test if two variables are related
Variables One categorical variable Two categorical variables
Expected Based on specified probabilities Based on row × column proportions
df Formula \(k - 1\) \((r-1)(c-1)\)
H₀ Data follows specified distribution Variables are independent

Common Ground:

  • Both use chi-square test statistic
  • Both require categorical data out.wi