Day 35

Math 216: Statistical Thinking

Bastola

Correlation & Simple Linear Regression

Key Question: How do two quantitative variables relate to each other? Let’s explore correlation and regression analysis!

Data Structure: Each case \(i\) has two measurements
- \(x_i\): explanatory variable (predictor)
- \(y_i\): response variable (outcome)
Real-World Examples:
- Temperature vs. cricket chirp rate
- Height vs. weight
- Study time vs. exam scores

Visualizing Relationships

Visualizing Relationships with Scatterplots:

A scatterplot shows the relationship between \((x_i, y_i)\) pairs, helping us understand:

Form: Is the relationship linear or non-linear?
Direction: Positive (upward slope), negative (downward slope), or no association?
Strength: How closely do points cluster around the trend?

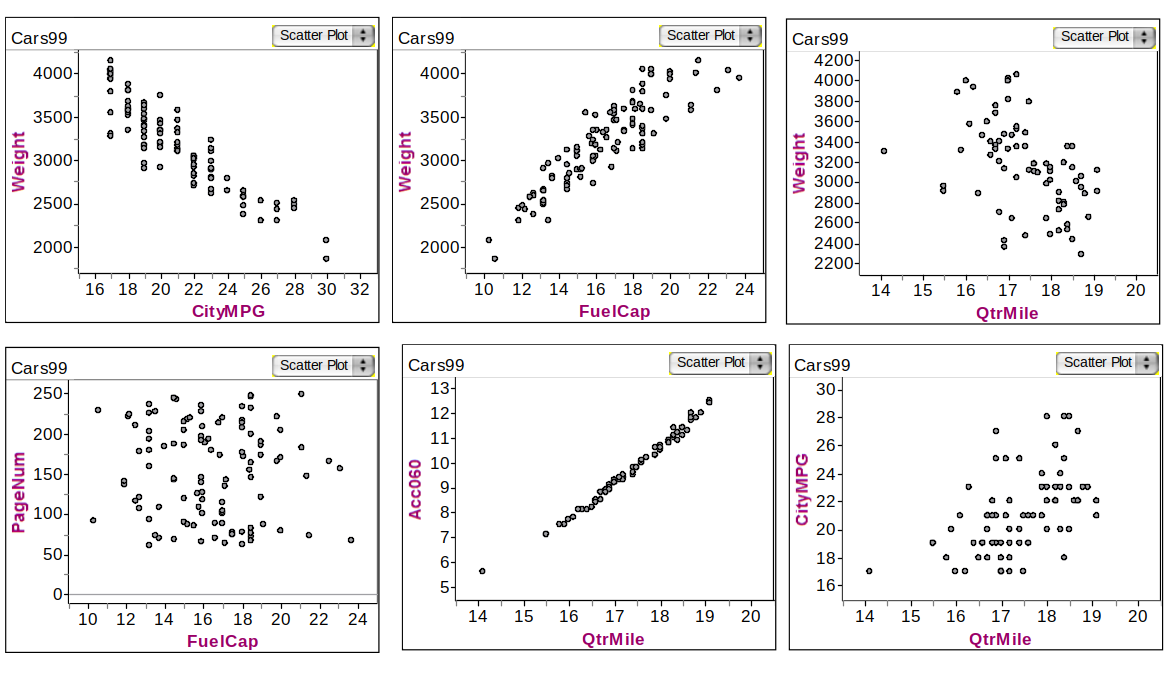
Example: Associations in Car dataset

Various Associations of quantitative variables in Cars data

Understanding Association Direction

Key Question: When one variable changes, what happens to the other?

Positive Association: As \(x\) increases, \(y\) increases
- Age of husband and age of wife
- Height and diameter of a tree
- Study time and exam scores
Negative Association: As \(x\) increases, \(y\) decreases
- Number of cigarettes smoked and lung capacity
- Depth of tire tread and miles driven
- Temperature and heating costs

Intuition: Positive relationships move together, negative relationships move apart!

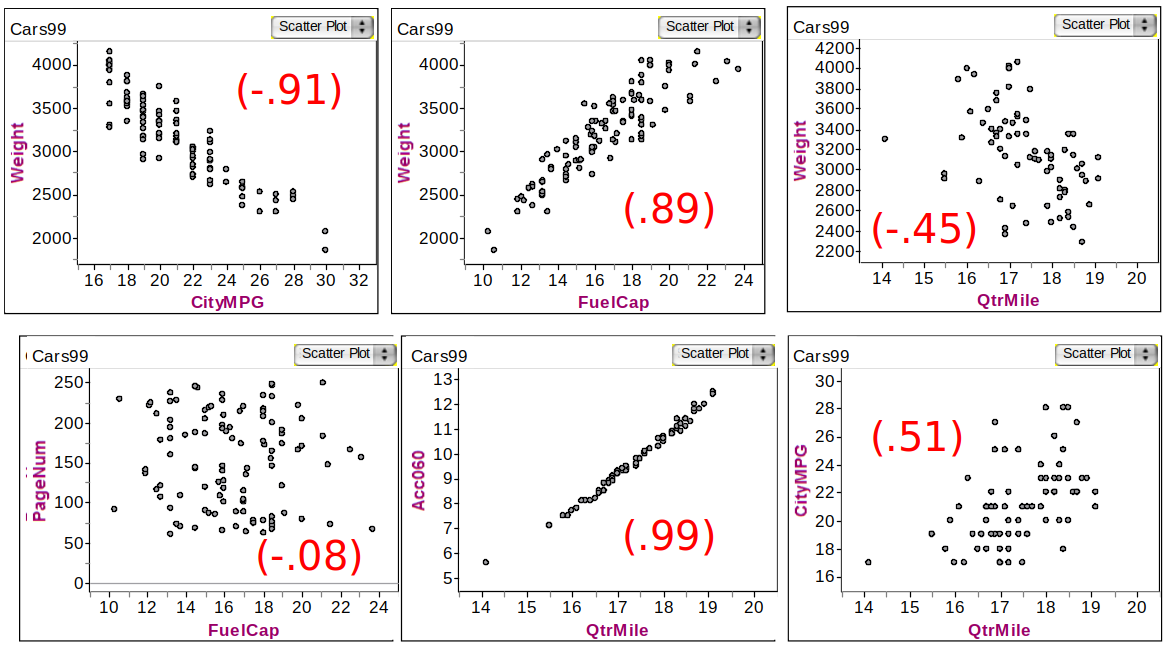
Understanding Correlation: The \(r\) and \(\rho\) Story

Key Question: How do we measure the strength and direction of linear relationships? Meet correlation coefficients!

Correlation Coefficients: \(r\) (sample) or \(\rho\) (population) quantify linear relationships
Strength Scale: \(r \approx \pm 1\) (strong), \(r \approx 0\) (weak)
Direction: Positive (\(r > 0\)) or negative (\(r < 0\)) linear association

The Correlation Formula: \[ r = \frac{\sum_{i=1}^n \left(\frac{x_i - \bar{x}}{s_x}\right) \left(\frac{y_i - \bar{y}}{s_y}\right)}{n-1} \]

Interpretation Guide:

\(r = 1\): Perfect positive linear relationship
\(r = -1\): Perfect negative linear relationship
\(r = 0\): No linear relationship

# R code to calculate correlation
cor(data$x, data$y)  # Simple but powerful!

Car Correlations

Correlations of various variables in Cars data

Correlation & Regression Decision Framework

flowchart LR
    %% Styling definitions
    classDef start fill:#FFFACD,stroke:#FF8C00,stroke-width:2px,color:#000
    classDef decision fill:#E6F3FF,stroke:#1E88E5,stroke-width:2px,color:#000
    classDef action fill:#E8F5E9,stroke:#43A047,stroke-width:2px,color:#000
    classDef endStyle fill:#FFEBEE,stroke:#E53935,stroke-width:2px,color:#000

    %% Nodes
    %% Added <br/> to A and D to save horizontal space
    A(["Start: Two<br/>Quantitative Variables"]):::start
    B{"Create<br/>Scatterplot"}:::decision
    C{"Linear<br/>Pattern?"}:::decision
    D{"Calculate<br/>Correlation r"}:::decision
    E{"Strong?<br/>|r| > 0.7"}:::decision
    F["Fit Linear<br/>Regression<br/>ŷ = b₀ + b₁x"]:::action
    G["Consider<br/>Non-linear<br/>Models"]:::action
    H["Weak Rel.<br/>No Linear<br/>Model"]:::action
    I["Interpret<br/>Slope &<br/>Intercept"]:::endStyle

    %% Flow connections
    A --> B
    B --> C
    C -->|Yes| D
    C -->|No| G
    D --> E
    E -->|Yes| F
    E -->|No| H
    F --> I
    G --> I
    H --> I

Figure 1: Regression Analysis Flowchart

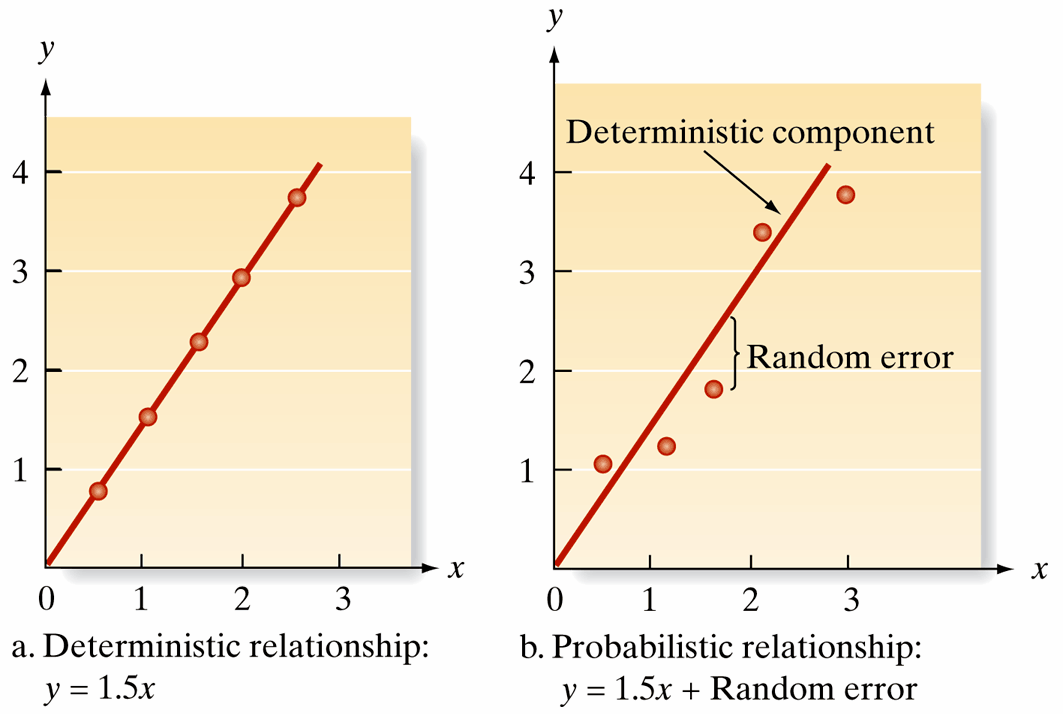
Deterministic vs. Probabilistic Models

Key Question: Are relationships in the real world perfectly predictable, or do we need to account for randomness?

Deterministic Model: Perfect, predictable relationships without error
- Example: \(y = 1.5x\) (always exactly 1.5 times x)
- Reality Check: Rarely exists in real-world data!
Probabilistic Model: Realistic relationships with randomness
- Example: \(y = 1.5x + \text{random error}\)
- General Form: \(y = \text{Deterministic component} + \text{Random error}\)
- Key Insight: Mean of random error is 0, so \(E(y)\) matches the deterministic component

Linear Regression Model

Key Question: How do we find the best straight line to describe our data? Welcome to linear regression!

Regression Equation: \(\hat{y} = b_0 + b_1x\)
- \(x\): explanatory variable (predictor)
- \(\hat{y}\): predicted response variable
Parameters:
- Slope (\(b_1\)): How much \(\hat{y}\) changes for each unit increase in \(x\) \[ b_1 = \frac{\text{change }\hat{y}}{\text{change } x} \]
- Intercept (\(b_0\)): Predicted \(y\) when \(x = 0\) \[ \hat{y} = b_0 + b_1(0) = b_0 \]

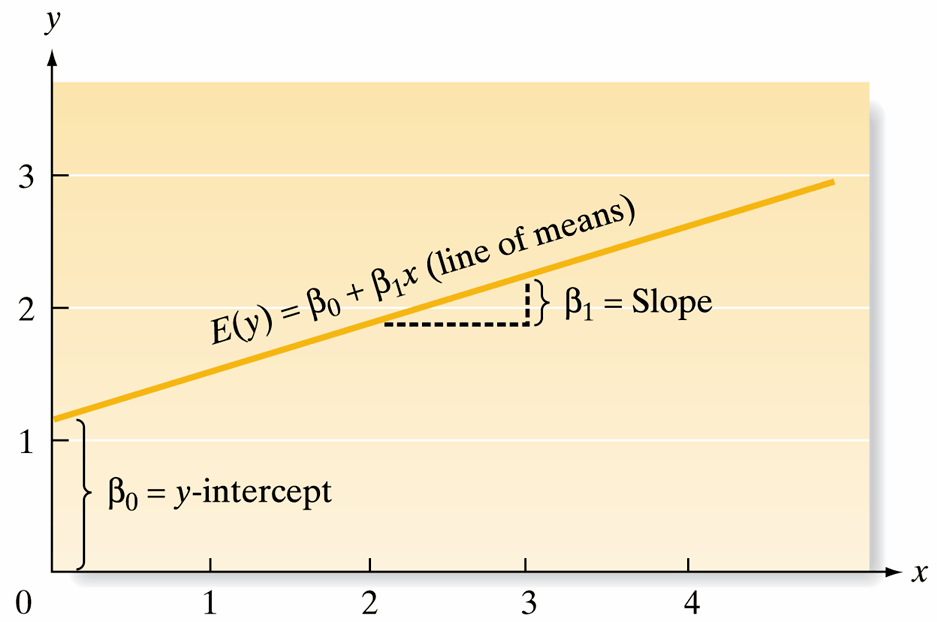
Simple Linear Regression: Fitting and Evaluation

Key Question: How do we actually find the “best” regression line?

Three-Step Process:
1. Hypothesize: Assume the deterministic component (e.g., \(E(y) = \beta_0 + \beta_1x\))
2. Estimate: Use least squares to find the best-fitting line
3. Evaluate: Assess model fit and use for prediction
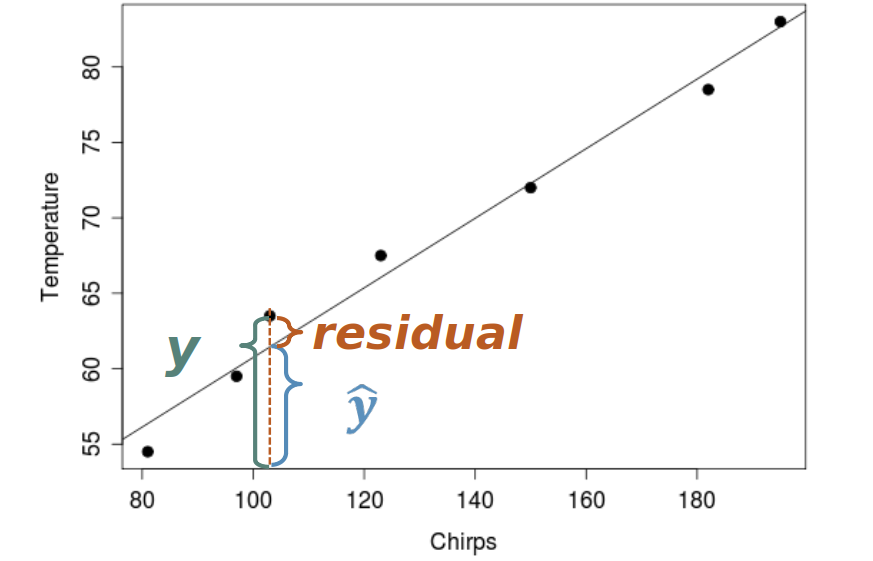
Residuals: The vertical distance from each point to the regression line
- Geometric Meaning: How far each point is from our “best guess” line
- Statistical Purpose: Help us measure how well our model fits the data

Residuals

Implementing Simple Linear Regression

Real-World Example: Can we predict cricket chirp rate from temperature?

Research Question: Does temperature affect how fast crickets chirp?
Model Approach: Use linear regression to predict chirp rate from temperature
Practical Application: This could help estimate temperature by listening to crickets!

Methodology:

Collect temperature and chirp rate data
Fit a linear model using least squares
Assess how well temperature predicts chirp rate
Use the model for temperature prediction

Data Overview

Observation	Temperature (°F)	Chirp Rate (chirps/15 sec)
1	89	20
2	72	16
3	93	20
4	84	18
5	81	17
6	75	16
7	70	15
8	82	17
9	69	15
10	83	16
11	80	15
12	83	17
13	81	16
14	84	17
15	76	14

Step-by-Step: Cricket Chirp Analysis with lm()

Let’s analyze the cricket chirp data step by step using R’s lm() function!

# Create cricket chirp dataset
cricket_data <- data.frame(
  temperature = c(89, 72, 93, 84, 81, 75, 70, 82, 69, 83, 80, 83, 81, 84, 76),
  chirp_rate = c(20, 16, 20, 18, 17, 16, 15, 17, 15, 16, 15, 17, 16, 17, 14)
)

# Display first few rows
head(cricket_data)

  temperature chirp_rate
1          89         20
2          72         16
3          93         20
4          84         18
5          81         17
6          75         16

Step 1: Visualize the Relationship

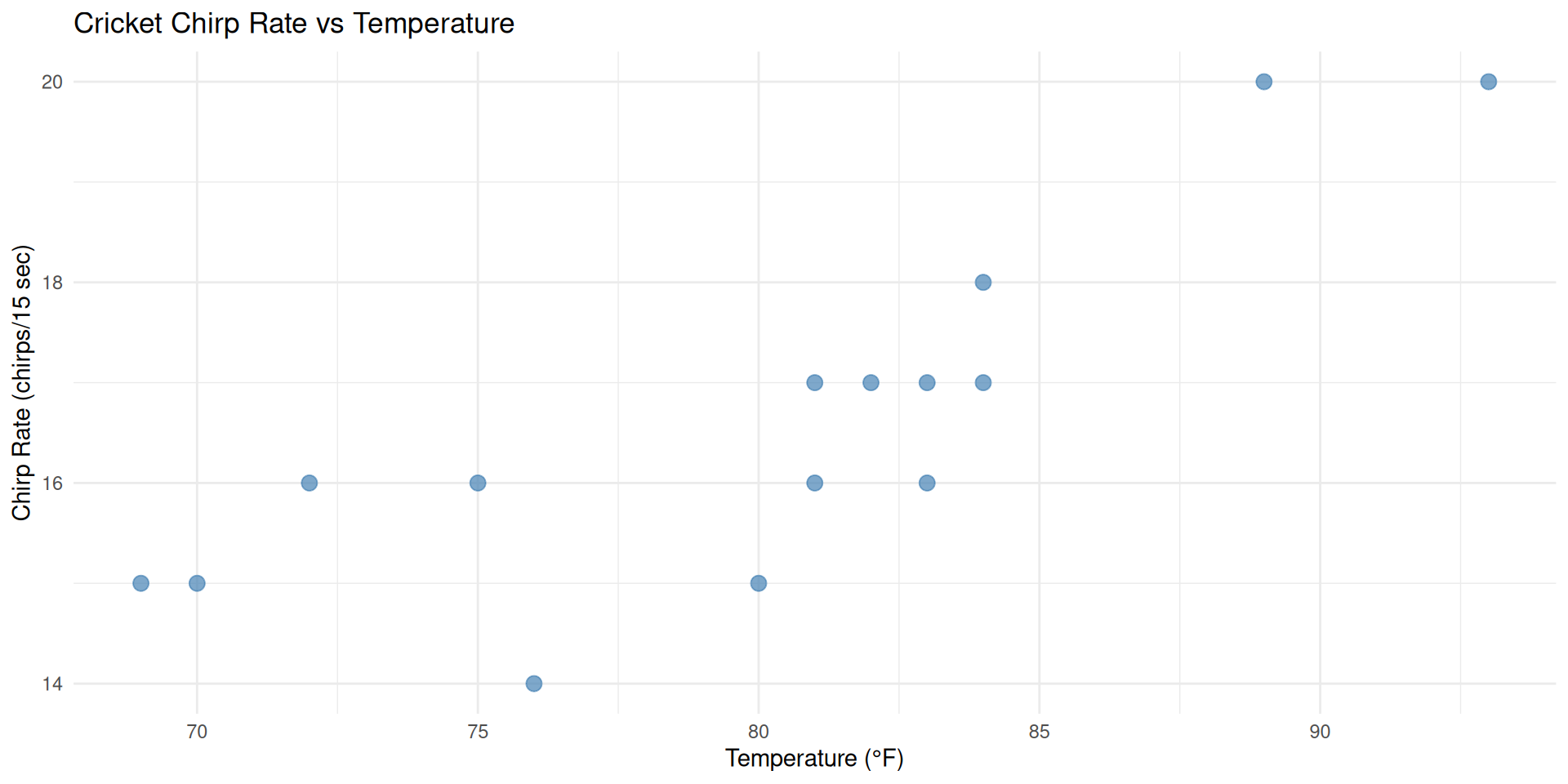
Step 1: Create Scatterplot

First, let’s visualize the relationship between temperature and chirp rate with a scatterplot.

Observation

We can see a clear positive linear relationship - as temperature increases, chirp rate also increases!

Step 2: Fit Linear Regression Model

Step 2: Fit Linear Model

Now let’s fit a linear regression model using R’s lm() function.

# Fit linear regression model
chirp_model <- lm(chirp_rate ~ temperature, data = cricket_data)
summary(chirp_model) # Display model summary


Call:
lm(formula = chirp_rate ~ temperature, data = cricket_data)

Residuals:
    Min      1Q  Median      3Q     Max 
-1.7246 -0.6013  0.2164  0.6280  1.5221 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept) -0.37210    3.23064  -0.115 0.910064    
temperature  0.21180    0.04018   5.271 0.000151 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 1.01 on 13 degrees of freedom
Multiple R-squared:  0.6812,    Adjusted R-squared:  0.6567 
F-statistic: 27.78 on 1 and 13 DF,  p-value: 0.0001513

Step 3: Add Regression Line to Scatterplot

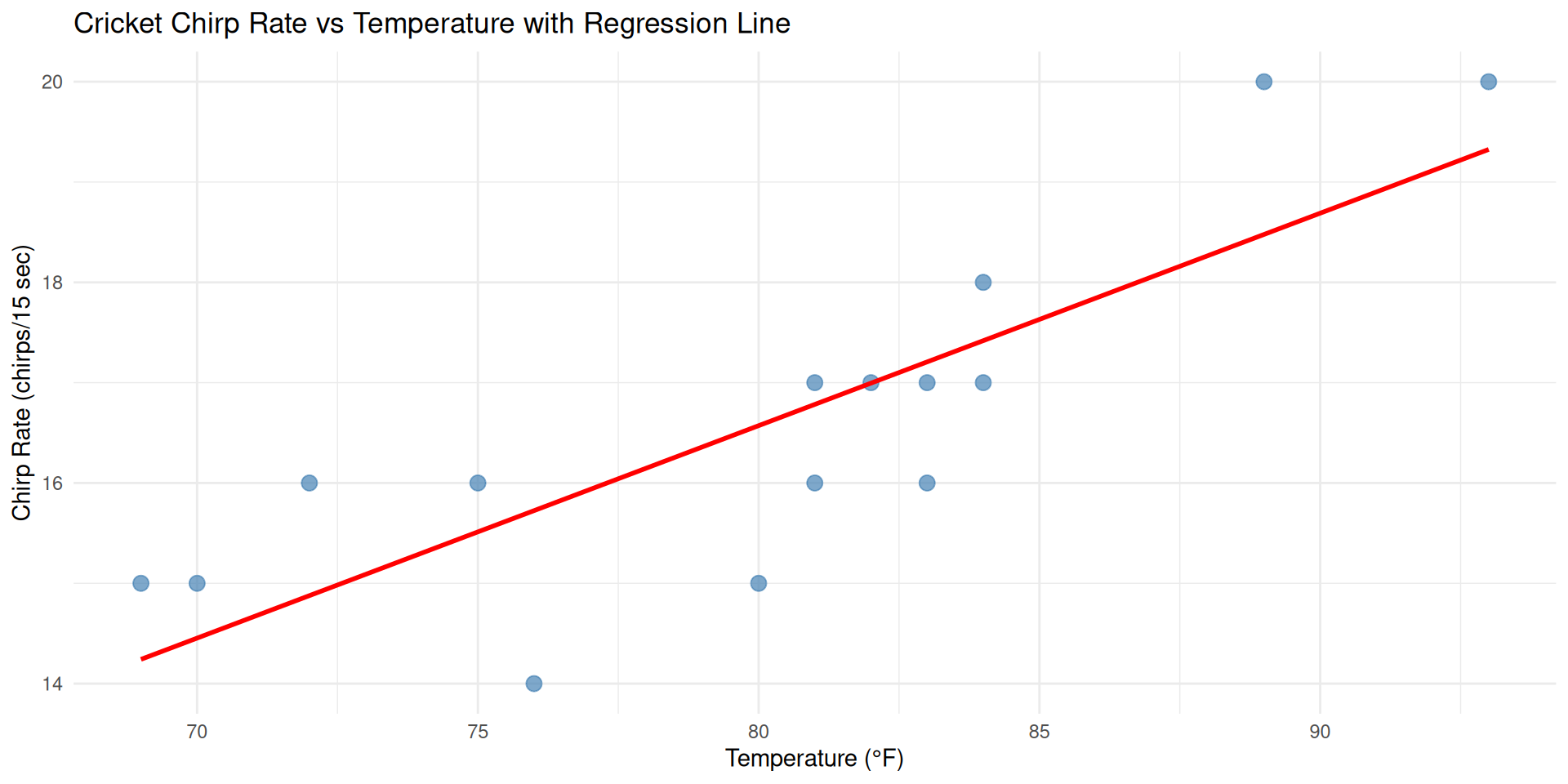
Step 3: Overlay Regression Line

Let’s add the regression line to our scatterplot to visualize the model fit.

Visual Assessment

The red line shows our best-fit linear model. Points are generally close to the line, indicating a good fit!

Step 4: Visualize Residuals

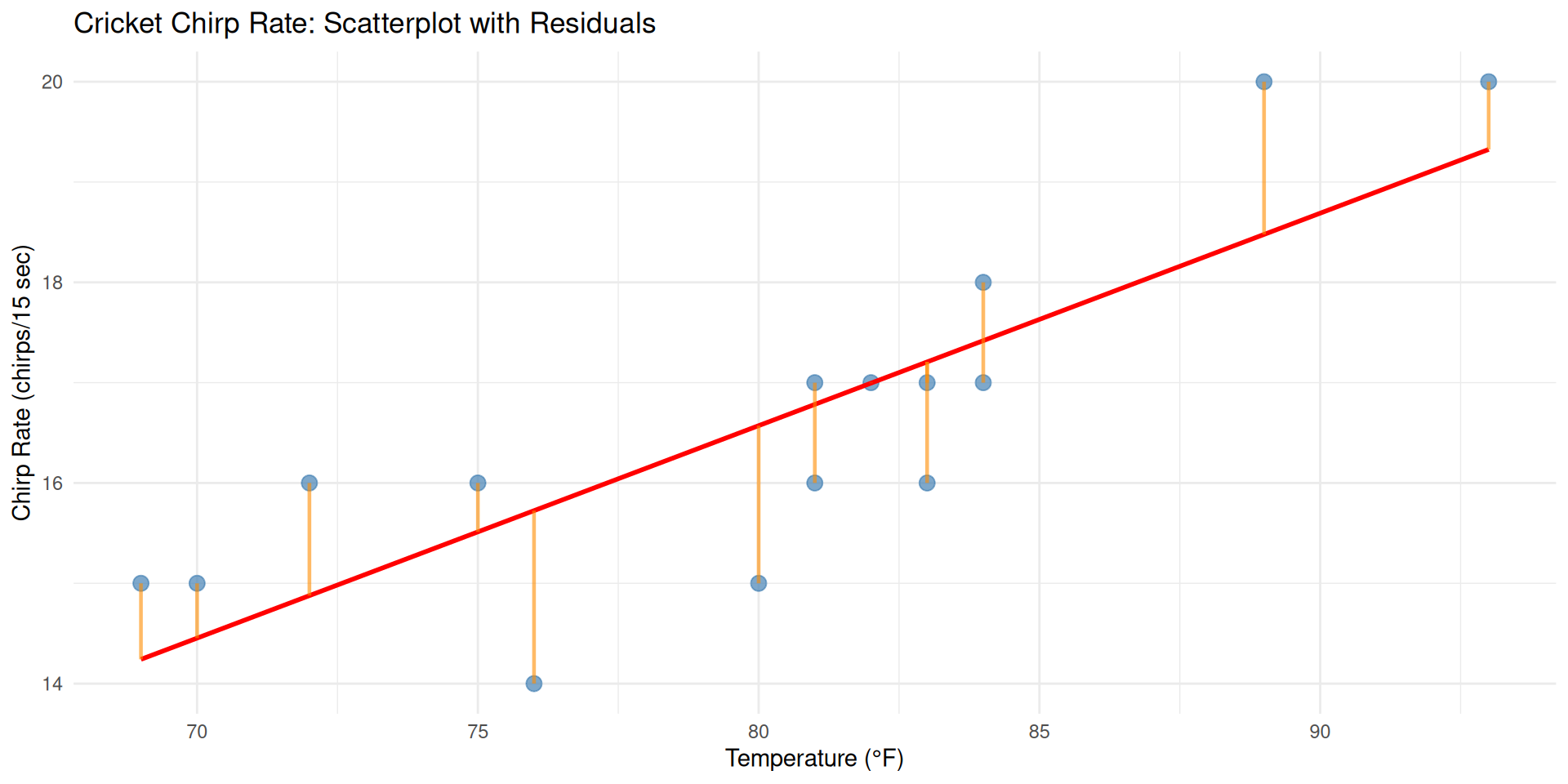
Step 4: Examine Residuals

Now let’s visualize the residuals - the vertical distances from each point to the regression line.

Understanding Residuals

The orange lines show residuals - how far each observation is from our prediction. Smaller residuals mean better model fit!

Summary: Cricket Chirp Analysis

Key Takeaways from our lm() analysis:

Strong Positive Relationship: Temperature strongly predicts cricket chirp rate
Model Equation: \(\hat{y} = -0.372 + 0.212x\)
Good Fit: R² = 0.681 (68.1% of variation explained)
Practical Application: Can predict chirp rate from temperature

lm() Function Benefits:

Simple syntax: lm(y ~ x, data)
Comprehensive output with coefficients, R², and significance
Easy to extract predictions and residuals
Foundation for more complex statistical modeling

Observation	Temperature (°F)	Chirp Rate (chirps/15 sec)
1	89	20
2	72	16
3	93	20
4	84	18
5	81	17
6	75	16
7	70	15
8	82	17
9	69	15
10	83	16
11	80	15
12	83	17
13	81	16
14	84	17
15	76	14

Observation	Temperature (°F)	Chirp Rate (chirps/15 sec)
1	89	20
2	72	16
3	93	20
4	84	18
5	81	17
6	75	16
7	70	15
8	82	17
9	69	15
10	83	16
11	80	15
12	83	17
13	81	16
14	84	17
15	76	14

Observation	Temperature (°F)	Chirp Rate (chirps/15 sec)
1	89	20
2	72	16
3	93	20
4	84	18
5	81	17
6	75	16
7	70	15
8	82	17
9	69	15
10	83	16
11	80	15
12	83	17
13	81	16
14	84	17
15	76	14