Activity 10

MATH 216: Statistical Thinking

Poisson Distribution Practice

Time Allocation: 15 minutes total

Part 1: Poisson Parameter Identification (5 minutes)

Blue Whale Research: Weekly sightings average = 2.6

Identify:

\(\lambda\) (mean) = _________________________
Theoretical \(\sigma\) = _____________________

Calculate Probabilities:

\(P(\text{exactly 5 sightings})\) = _________________________
\(P(\text{fewer than 2 sightings})\) = ______________________

Multiple Choice: Given \(\lambda = 4\), \(P(X=2)\) = ?

□ 0.1465
□ 0.1954
□ 0.2381
□ 0.2707

Part 2: Poisson Pattern Analysis (5 minutes)

Simulated Whale Data Summary:

set.seed(123)
whale_sightings <- rpois(52, lambda = 2.6)

Weekly whale sightings: histogram (left) and summary statistics (right).

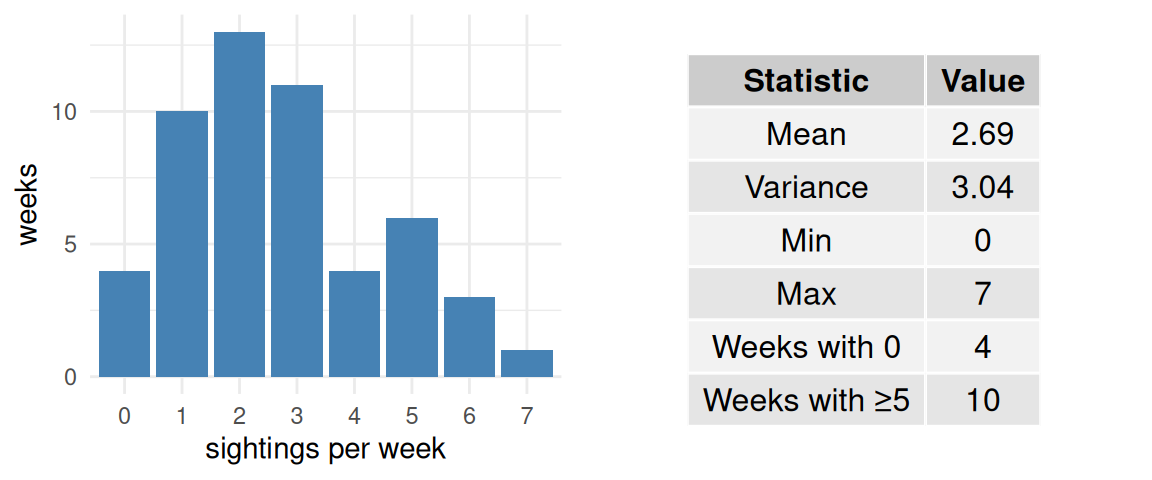
Analysis:

Empirical mean vs theoretical λ: ___________________
Variance/mean ratio: _____________________________
Does data appear Poisson? □ Yes □ No
Evidence: _______________________________________

Part 3: Traffic Safety Application (5 minutes)

Hypothetical Scenario: Monthly accidents at intersection - \(\lambda = 3\) accidents per month

Calculate:

\(P(\text{exactly 5 accidents in month})\) = __________________
\(P(\text{no accidents in month})\) = _______________________
\(P(\text{more than 5 accidents in month})\) = ________________

Safety Planning:

If \(P(>5 \text{ accidents}) > 0.05\), additional safety measures needed
Recommendation: □ Implement measures □ No action needed
Reasoning: _______________________________________