Activity 4

MATH 216: Statistical Thinking

Distribution Analysis & Z-Scores

Time Allocation: 15 minutes total

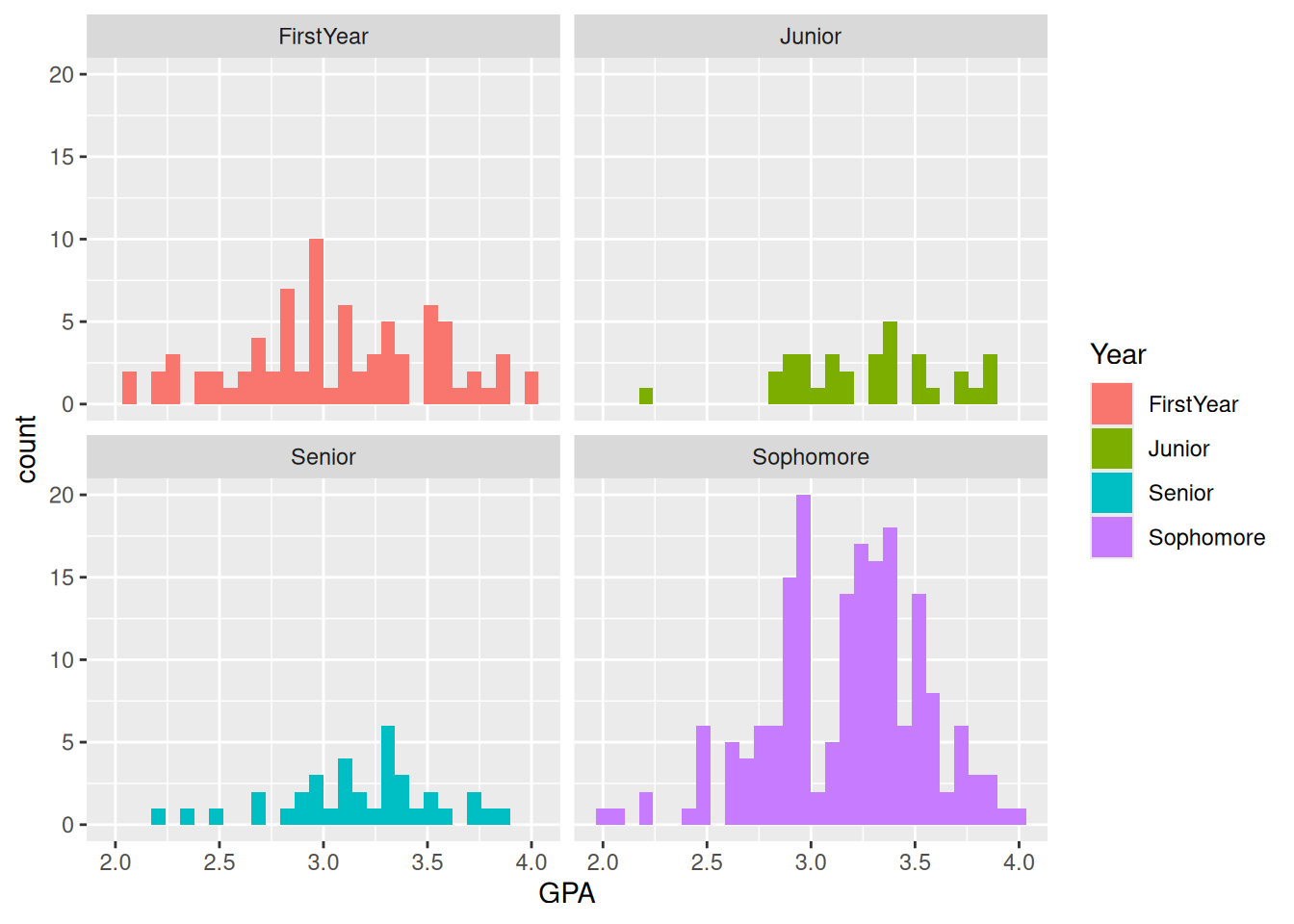
  1. Case Study: Use the graphical and numerical summaries of Student Survey Dataset to compare the GPA of students for different Year.
survey_data <- read.csv("https://raw.githubusercontent.com/deepbas/datasets/main/StudentSurvey.csv") |>
   tidyr::drop_na()

ggplot(survey_data, aes(x=GPA, fill=Year)) +
  geom_histogram() +
  facet_wrap(~Year) 

survey_data |> 
  group_by(Year) |> 
  summarize(mean = mean(GPA),
            sd = sd(GPA),
            n = n()) |> 
  knitr::kable(caption = "Summary Statistics of GPA for all Years")
Summary Statistics of GPA for all Years
Year mean sd n
FirstYear 3.070759 0.4702584 79
Junior 3.273636 0.3688057 33
Senior 3.171667 0.3754274 36
Sophomore 3.173224 0.3690737 183

Part 1: Distribution Concepts (5 minutes)

Instructions: Provide examples and explanations for each concept:

  1. Symmetric Distribution Example: _________________________

    • Why it’s symmetric: ____________________________________

  2. Real-world skewed distribution: _________________________

    • Direction of skew: □ Left □ Right
    • Reason for skew: ______________________________________

  3. Normal distribution characteristic: ______________________

Part 2: Z-Score Interpretation (5 minutes)

Scenario: A student’s GPA has a z-score of 2.

  1. What does this mean?

    • □ GPA is 2 points above mean
    • □ GPA is 2 standard deviations above mean
    • □ GPA is 2 standard deviations below mean
    • □ GPA is 2 points below mean

  2. Explanation: __________________________________________

  3. If mean GPA = 3.0 and SD = 0.5, calculate actual GPA:

    • Formula: _________________________
    • Calculation: ______________________
    • Actual GPA: ______________________

Part 3: Data Analysis (5 minutes)

Analysis Questions:

  1. Which year has the highest average GPA? __________________

  2. Potential explanation for this pattern:

  3. Two potential biases in this dataset: