Activity 17
MATH 216: Statistical Thinking
Central Limit Theorem and Standard Error
Time Allocation: 15 minutes total (5 min reading, 10 min individual work)
Part 1: Conceptual Understanding (3 minutes)
Instructions: Answer the following questions about the Central Limit Theorem:
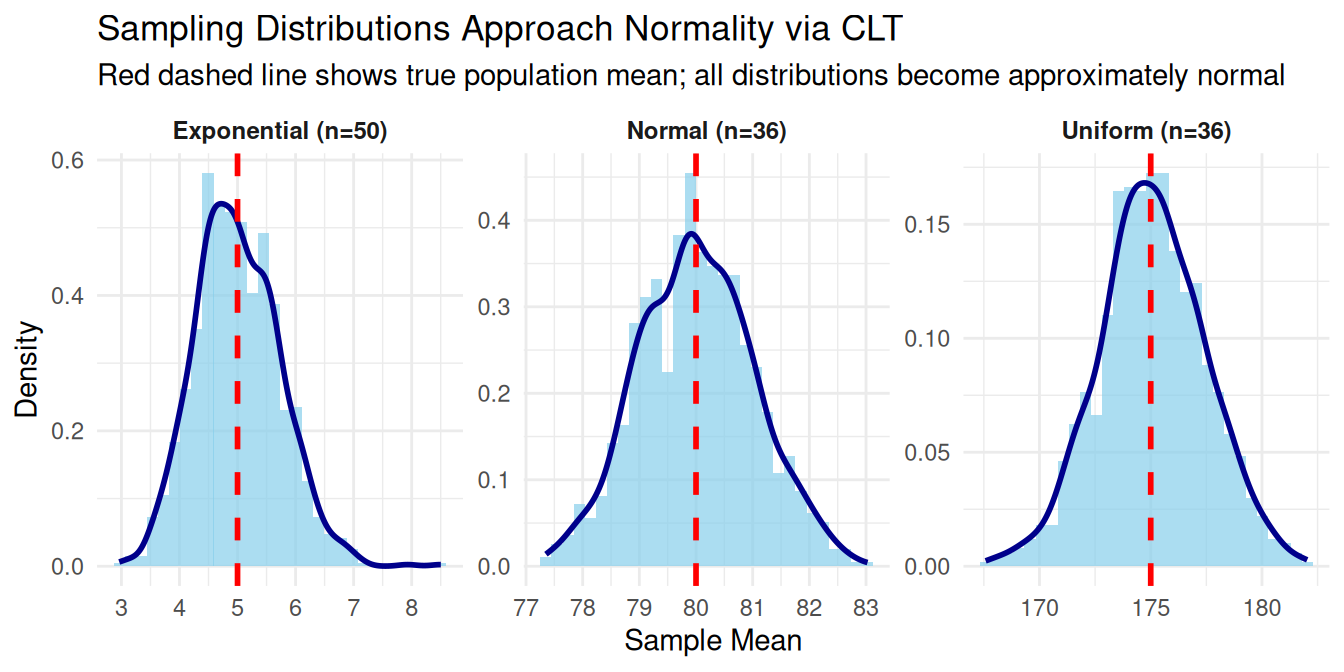
- What is the Central Limit Theorem and why does it allow us to use normal distributions for inference?
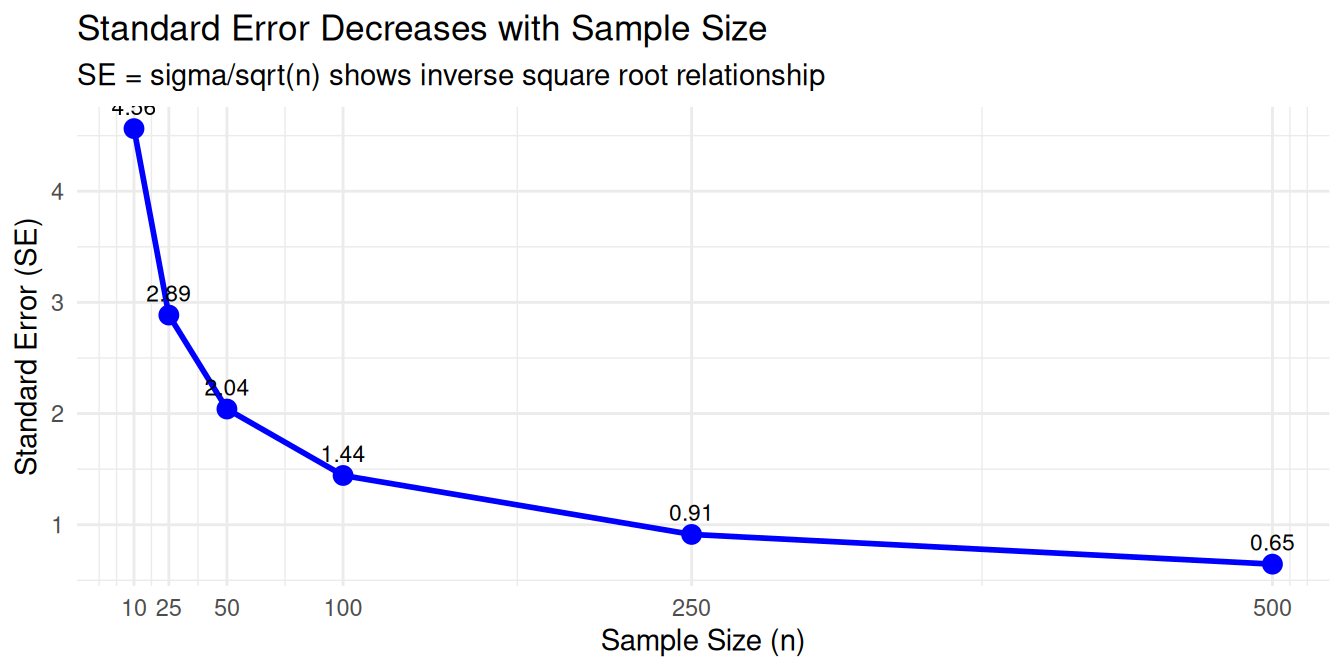
- How does the standard error relate to sample size and population standard deviation?
- Why can we apply the CLT to non-normal populations (uniform, exponential) with sufficiently large samples?
Part 2: Standard Error Calculations (4 minutes)
Formula: Standard error \(\sigma_{\bar{x}} = \frac{\sigma}{\sqrt{n}}\)
Calculate the following:
Steel sheets: Population \(\sigma = 14.43\) mm, sample size \(n = 36\)
Standard error = mm
Population study: \(\mu = 80\), \(\sigma = 6\), \(n = 36\)
\(\mu_{\bar{x}}\) = , \(\sigma_{\bar{x}}\) =
College students: \(\mu = 25\) years, \(\sigma = 9.5\) years, \(n = 125\)
\(\mu_{\bar{x}}\) = , \(\sigma_{\bar{x}}\) =
Customer arrivals (exponential): \(\mu = 5\) min, \(\sigma = 5\) min, \(n = 50\)
\(\mu_{\bar{x}}\) = , \(\sigma_{\bar{x}}\) =
Show your work for problems 1 and 4:
Part 3: Probability Applications (3 minutes)
Using the Central Limit Theorem, calculate the following probabilities:
Steel sheets: Uniform(150, 200) mm, \(\mu = 175\) mm, \(\sigma = 14.43\) mm, \(n = 36\)
\(P(\bar{x} > 180\) mm) =
Population study: \(\mu = 80\), \(\sigma = 6\), \(n = 36\)
\(P(\bar{x} > 82)\) =
College students: \(\mu = 25\), \(\sigma = 9.5\), \(n = 125\)
\(P(\bar{x} > 26)\) =
Show your work for problem 1 (calculate z-score and use normal table):
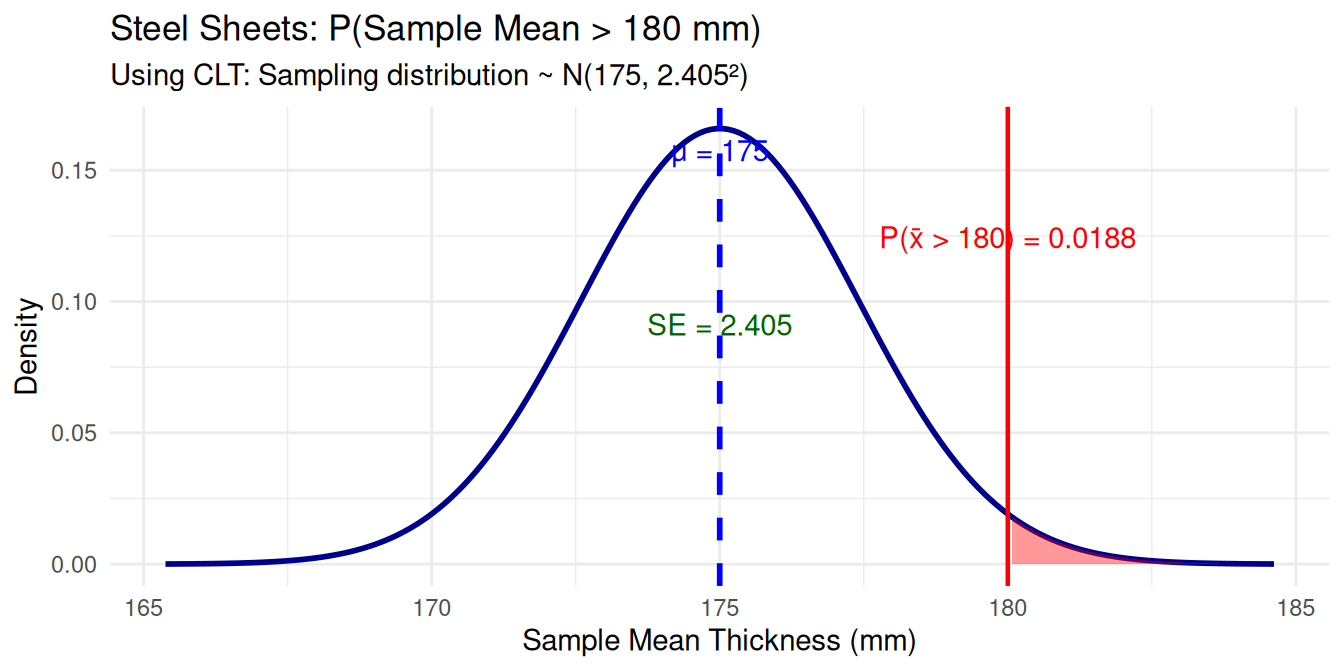
Critical Thinking: Why can we use the normal distribution for the steel sheets example even though the population has a uniform (non-normal) distribution?