Activity 16
MATH 216: Statistical Thinking
Statistical Estimation and Unbiasedness
Time Allocation: 15 minutes total (5 min reading, 10 min individual work)
Part 1: Conceptual Understanding (3 minutes)
Instructions: Answer the following questions about statistical estimation:
- Why is unbiasedness important in statistical estimation?
- What is the trade-off between bias and variance in estimators?
- What does standard error measure in sampling distributions?
Part 2: Estimator Comparison (4 minutes)
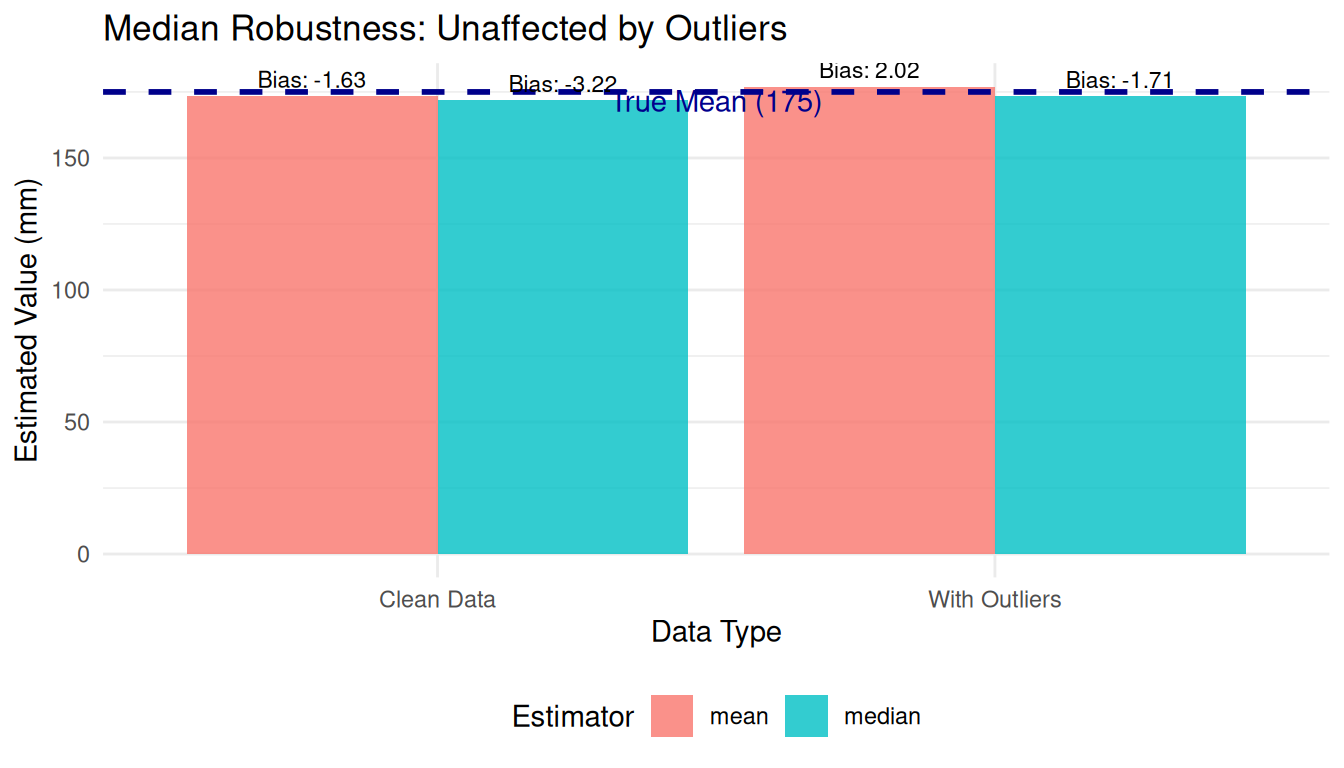
Scenario: Steel sheets have thickness following uniform distribution (150-200 mm). Two statistics estimate the population mean:
- Sample mean (\(\bar{x}\))
- Sample median (M)
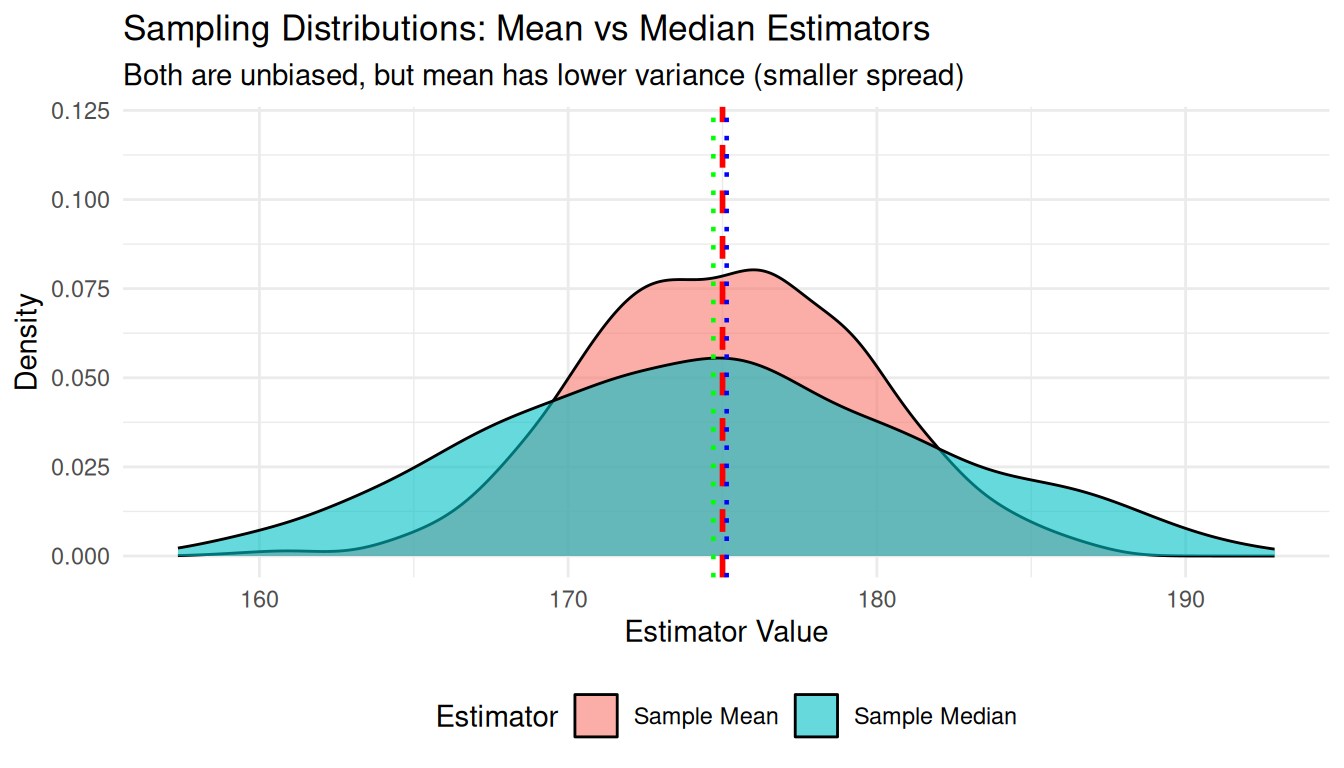
Based on sampling distributions, which estimator is better and why?
Calculate expected properties:
- True population mean = mm
- Expected bias of sample mean =
- Expected bias of sample median =
- Which estimator is unbiased?
- Which estimator has lower variance?
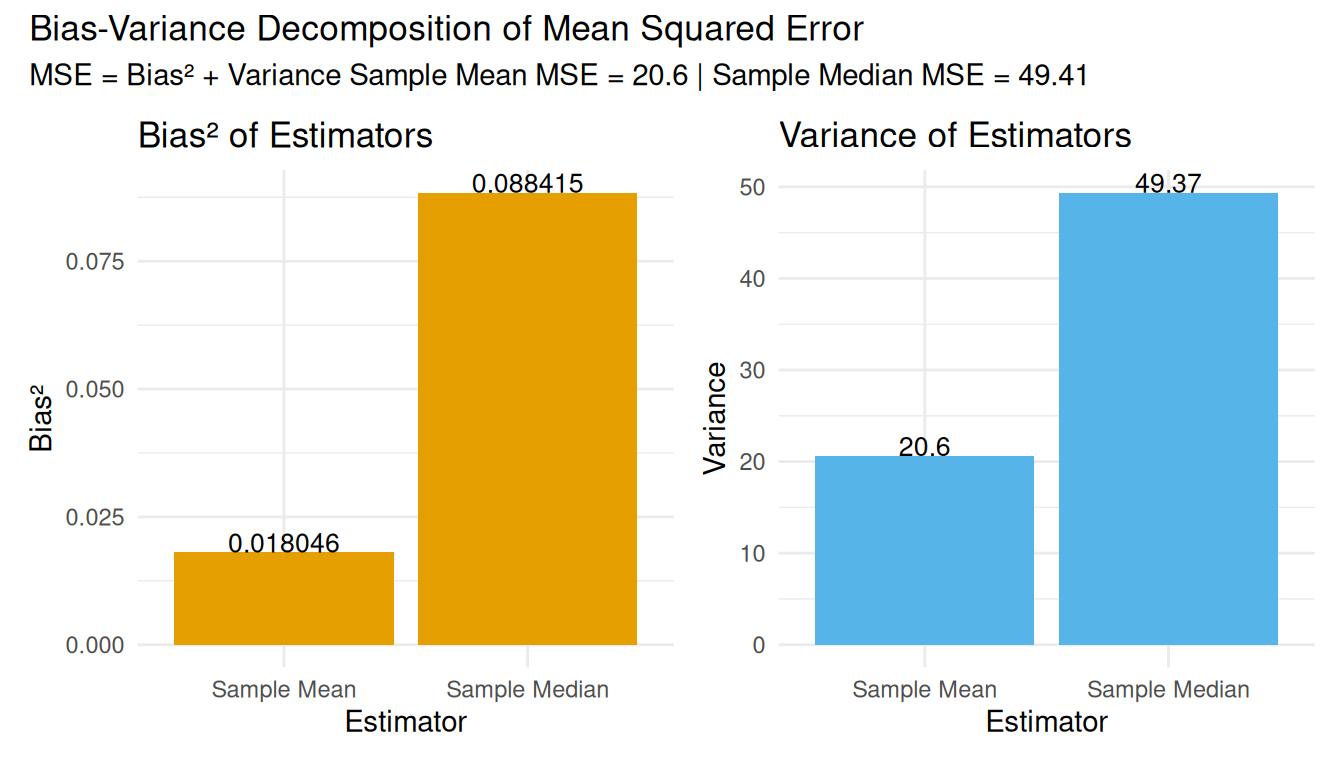
| Estimator | Mean | Std Error | Bias | MSE |
|---|---|---|---|---|
| Sample Mean | 175.13 | 4.54 | 0.13 | 20.60 |
| Sample Median | 174.70 | 7.03 | -0.30 | 49.41 |
Part 3: Real-World Application (3 minutes)
Quality Control Scenario: A factory needs to estimate average steel thickness for quality assurance.
Decision Analysis:
- Would you prefer an unbiased estimator with high variance or a slightly biased estimator with low variance? Why?
- What practical considerations might influence this choice in a manufacturing setting?
Critical Thinking: When might the median be preferred over the mean, even if it’s biased?